7 Channel couplings

The coupling terms V_ij need to be determined for common reaction mechanisms such as inelastic excitations of nuclei, or particle transfers from the projectile to/from the target.

7.1 Nuclear Rotational Model

Consider one deformed nucleus with deformation lengths $\delta_\lambda$, (the fractional deformation $\beta_\lambda$ times some average radius R_c). The effect of these deformations can be expressed as a change in the radius at which we evaluate the optical potentials, the change depending on the relative orientations of the radius vector to the intrinsic orientation of the nucleus. When U(R) is the potential shape to be deformed, the coupling interaction is

$${\bf V}( {\bf\xi} , {\bf R}) = U(R - \delta( \hat{\bf R}, {\bf\xi} ))$$ (42)

where the `shift function' has the multipole expansion

$$\delta( \hat{{\bf R}'}) = \sum_{\lambda \neq 0} \delta_\lambda Y^0_\lambda (\hat{{\bf R}'})$$ (43)

($\hat {\bf R}'$ is the vector $\hat{\bf R}$ rotated to the body-centred frame of coordinates defined by ${\bf\xi}$). Transforming to the space-fixed frame of reference, and projecting onto the spherical harmonics, the multipole expansion becomes

$${\bf V}( {\bf\xi} , {\bf R}) \sum_{\lambda \mu} {\sf V}_\lambda^N (R) D^\lambda_{\mu 0} Y^\mu_\lambda (\hat{\bf R})$$ =

$$\mbox{where } {\sf V}_\lambda^N (R) 2\pi \int _{-1}^{+1} U(~r(R,\cos \theta)~) Y_\lambda^\mu (\theta ,0) ~d(\cos \theta)$$ =

$$\mbox{and } r(R,u) R - \sum_\lambda\sqrt{ {2 \lambda+1 \over 4 \pi} } P_\lambda (u) \delta_\lambda + \epsilon$$ =

$$\mbox{with } \epsilon {\sum _ \lambda {\delta_\lambda}^2} / (4 \pi R_c )$$ =

The correction 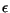$\epsilon$ is designed ([8]) to ensure that the volume integral of the nuclear monopole potential ${\sf V}_0 ^N(R)$ is the same as that of U(R), and is correct to second order in the $\{\delta_\lambda\}$. When the $\{\delta_\lambda\}$ are small, the above multipole functions are simply the first derivatives of the U(R) function:

$${\sf V}_\lambda^N (R) = - {\delta_\lambda \over \sqrt {4 \pi}} ~{dU(R) \over dR} ,$$ (44)

with the same shape for all nuclear multipoles $\lambda> 0$. The deformations of the Coulomb potential can also be defined by the $\delta_\lambda$, but more accurately by means of the Coulomb reduced matrix element $\langle I' \Vert E \lambda \Vert I\rangle$ that is directly related to electromagnetic decay strengths as $\pm\sqrt { (2I+1) B(E \lambda , I \rightarrow I') }$. The reduced matrix element defined by the Wigner-Eckart theorem of the form.

$$\langle j_f m_f \vert \hat{O}_{j m} \vert j_i m_i\rangle = ... ...ngle \langle j_f \vert\vert \hat{O}_j \vert\vert j_i\rangle$$ (45)

For a rotational model of the nucleus, the matrix element is determined to first order in $\delta_\lambda$ by

$$\langle I' \Vert E \lambda \Vert I\rangle = {3Z \delta_\lambda {R... ...lambda-1} \over 4 \pi} ~ \sqrt {2I+1} ~~\langle I K \lambda 0 \vert I' K\rangle$$ (46)

for transitions from a state of spin I to one of spin I' in a rotational band of projection K in a nucleus of charge Z. The radial form factors for Coulomb inelastic processes are derived from the multipole expansion of $\vert {\bf r}- {\bf r}' \vert^{-1}$, giving for interactions with the other nucleus (charge Z') of

$${\sf V}_\lambda^C (R) = \langle I' \Vert E \lambda \Vert I\rangle... ...R \leq R_c)}\\ {1 / R^{\lambda+1} \ \ \ \ \ \ (R> R_c) } \end{array} \right. ~$$ (47)

Note that, especially for dipole and quadrupole couplings ($\lambda=1,2$), these Coulomb couplings have a long range that is much larger than the sum of the radii of the interacting nuclei. Any method for numerically solving the coupled equations with these couplings has to include some particular treatment of these couplings at large distances as discussed in ref. [16]. For projectile inelastic excitations, the coupling matrix elements between different partial waves defined with Eq. (30) are

$$\langle (L J_p)J, J_t ; J_T \vert {\bf V}_\lambda \vert (L' J'_ p)J , J_ t ; J_T\rangle = {\bf X}^{J \lambda}_{LJ_p :L' J'_ p} (R)$$ (48)

whereas for target excitations,

$$\langle (L J_p)J, J_t ; J_T \vert {\bf V}_\lambda \vert (L' J_ p)J' , J'_ t ; J_T\rangle = (-1)^{J-J' -L+L'} \hat J \hat {J'}$$

$$\times \sum_{J_2} (2J_2 + 1) W(J_p L J_T J _t ; J J_2) W(J_p L' J_T J'_ t ; J' J_2)$$

$$\times \ \ \ {\bf X}^{J_2 \lambda}_{LJ_t :L' J'_ t} (R)$$

having defined the `spatial' couplings as

$${\bf X}^{J \lambda}_{LI:L' I'} (R) \hat L \hat {L'} (-1)^{J-I' -L+L'} W(L L' I I' ; \lambda J) \langle L 0 L' 0 \vert \lambda 0\rangle$$ =

$$~~ \left [ {\sf V}_\lambda^C (R) + \hat{I'} \langle I'K\lambda 0\vert IK\rangle {\sf V}_\lambda^N (R) \right ]$$ (49)

The rotational model factor $\hat{I'} \langle I'K\lambda 0\vert IK\rangle$ has been built into the definition of the Coulomb reduced matrix element.

7.2 Rearrangement Reactions

7.2.1 Spectroscopic amplitudes and factors

If the nuclear state 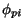$\phi_{pi}$ is transformed into state 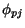$\phi_{pj}$ by removal of some nucleon(s), then we can define an overlap wave function

$$\chi^p_{j:i}({\bf r}) = \langle \phi_{pj}(\xi_{pj}) \vert \phi_{pi}(\xi_{pj},{\bf r})\rangle$$ (50)

The partial wave components of this overlap can be written as the sum of some amplitudes A times normalised wave functions $\varphi$. The coefficients A are called spectroscopic amplitudes (or coefficients of fractional parentage), and their square moduli |A|² the spectroscopic factors. If a coupling order $\left \vert ( \ell s)j,I;~JM \right\rangle$ is used, the composite nucleus wave function is

$$\phi_{JM} ( \xi_{pj} , {\bf r}) = \frac{1}{\sqrt{n_{pi}}}\sum_{\e... ...}^{jIJ} ~ \left [\phi_I(\xi_{pj}) \varphi_{\ell sj} ({\bf r}) \right ]_{JM} \ ,$$ (51)

and

$$S_{\ell sj}^{jIJ} = \vert A_{\ell sj}^{jIJ}\vert^2$$ (52)

is the spectroscopic factor. The n_pi is again the number of nucleons (or clusters) in the composite system $\phi_{pi}$ that are identical to that transferred, and the n_pi^-1/2 factor arises because of the normalisation of antisymmetrised wave functions for the core and composite nuclei. (In many common reactions with or near closed shell nuclei, the n_pi^-1/2 factor cancels some of the n! terms in eqs. (19,21)). Similar target overlap wave functions can also be defined.

7.2.2 Transfer couplings

To calculate the coupling term that arises when a particle is transferred, for example from a target bound state to being bound in the projectile, we need to evaluate matrix elements where the initial (primed) state has a composite target with internal coordinates $\xi'_ t \equiv \{ \xi_t , {\bf r}' \}:$ $\phi_{J'_ t} (\xi_t , {\bf r}' ) = \vert ( \ell' s) j' , J_t ; J'_ t\rangle$ and the final (unprimed) state has a composite projectile with internal coordinates $\xi_p \equiv \{ \xi_{p'} , {\bf r}\}:$ $\phi_{J_p} (\xi'_ p , {\bf r}) = \vert ( \ell s) j , J'_ p ; J_p\rangle .$ Let ${\bf V}$ be the interaction potential, of which the prior form is

$${\bf V} = V_{\ell sj} ({\bf r}) + U_{cc} (R_c) - U_{\alpha'} ({\bf R}')$$ (53)

and the post form is

$${\bf V} = V_{\ell' sj'} ({\bf r}') + U_{cc} (R_c) - U _\alpha ({\bf R})$$ (54)

where $V_\beta ({\bf r})$ is the potential which binds $\varphi_\beta ({\bf r}),$ $U _\alpha ({\bf R})$ are the optical potentials, and $U_{cc} ({\bf R}_c)$ is the `core-core' potential, here between the p' and the t nuclei. The $V_\beta$ will be real, but the $U _\alpha$ and U_cc will typically have both real and imaginary components. The matrix element is now a non-local integral operator, as it operates on the function $f_{\alpha'} (R' )$ to produce a function of R. This section therefore derives the non-local kernel $V_{\alpha ,\alpha'} (R,R' )$ so that the matrix element operation on a wave function, which initially involves a five dimensional integral over ${\bf r}$ and $\hat{\bf R}$, may be calculated by means of a one-dimensional integral over R':

$$\int_ 0 ^ {R_m} V_{\alpha ,\alpha'} (R,R' ) f_{\alpha'} (R' ) dR' .$$ (55)

Note that when the initial and final single-particle states are real, then the kernel function is symmetric

$$V_{\alpha ,\alpha'} (R,R') = V_{\alpha' ,\alpha} (R',R)\ .$$ (56)

When the potential V contains only scalar potentials, the kernel calculation can be reduced to the problem of finding the spatial part ${\bf X}^\Lambda_{\ell L: \ell' L'} (R,R' )$ defined so that, given

$$\langle (LJ_p)J,J_t ;J_T \vert {\bf V}\vert(L' J'_ p)J' ,J'_ t ;J_T\rangle$$

$$=\sum_{\Lambda F} (-1)^{s+J'_ p - F} \hat J \hat {J'_ t} \hat j \... ...\begin{array}{ccc}L'&J'_p&J'\\ \ell'&s'&j'\\ \Lambda&F&J\end{array} \right \}$$

$$W(J_t j' J_T J' ;~ J'_ t J) W(ls J_p J'_ p ;~jF) W(L \ell J F;~ \Lambda J_p )$$

$$\langle \ell L; \Lambda \vert {\bf V} \vert \ell' L' ; \Lambda\rangle ,$$ (57)

the integral operator $\langle \ell L; \Lambda \vert {\bf V} \vert \ell' L' ; \Lambda\rangle$ has the kernel function ${\bf X}^\Lambda_{\ell L: \ell' L'} (R,R' ).$ Now the ${\bf r}$ and ${\bf r}'$ are linear combinations of the channel vectors ${\bf R}$ and ${\bf R}'$: ${\bf r}= a {\bf R}+ b {\bf R}'$ and ${\bf r}' = a' {\bf R}+ b' {\bf R}'$ where, when $\varphi_\ell ({\bf r})$ is the projectile bound state,

$$a = \nu_t \omega , ~~~ b = - \omega , ~~~ a' = \omega , ~~~ b' = - \nu_p \omega ,$$ (58)

with $\nu_p \equiv m_{pi'} / m_{pi}$ , $\nu_t \equiv m_{ti} / m_{ti'}$ , and $\omega = (1 - \nu_p \nu_t ) ^ {-1}$ . When $\varphi_\ell ({\bf r})$ is the target bound state

$$a = - \nu_p \omega, ~~~ b = \omega , ~~~ a' = - \omega , b' = \nu_t \omega , ~~~$$ (59)

with $\nu_p \equiv m_{pi} / m_{pi'}$ , $\nu_t \equiv m_{ti'} / m_{ti}$ , and $\omega = (1 - \nu_p \nu_t ) ^ {-1}$ . The `core-core' vector is always ${\bf R}_c = {\bf r}' - {\bf r} = (a' - a) {\bf R}+ (b' - b) {\bf R}' .$ Thus the spherical harmonics $Y_\ell ( \hat {\bf r})$ and $Y_{\ell'} ( \hat{\bf r}' )$ can be given in terms of the spherical harmonics $Y_n ( \hat{\bf R})$ and $Y_{n'} ( \hat{\bf R}' )$ by means of the Moshinsky[9] solid-harmonic expansion (see also refs. [10,11])

$$Y_\ell^m ( \hat {\bf r}) \sqrt {4 \pi} \sum_{n \lambda} c( \ell ,n) {(a R)^{\ell - n} (b R' )^n \over r^ \ell }$$ = (60)

$$Y_{\ell - n}^{m - \lambda} ( \hat{\bf R}) Y_n^\lambda ( \hat{\bf R}') \langle \ell - n m - \lambda n \lambda \vert \ell m\rangle$$ (61)

from ${\bf r}= a {\bf R}+ b {\bf R}'$, where

$$c( \ell ,n) = \left ( \frac{(2\ell + 1)!}{(2n+1)!(2(\ell-n)+1)!} \right )^{1/2} .$$

We now perform the Legendre expansion

$${\bf V} {u_{\ell sj} (r) \over r^{\ell +1}} ~ {u_{\ell' sj'} (r')... ...r {r'}^{\ell' +1} }~ = \sum _ T (2T+1) {\bf q}^T_ {\ell , \ell'} (R,R') P_T (u)$$ (62)

where the Legendre polynomials P_T (u) are functions of u, the cosine of the angle between ${\bf R}$ and ${\bf R}' ,$ by using r = (a² R² +b² R'² + 2abRR' u)^1/2 (with r' analogously) in the numerical quadrature of the integral

$${\bf q}^T_ {\ell , \ell'} (R,R') = \frac{1}{2}\int_ {-1} ^ {+1} {... ...(r)\over r^{\ell + 1}} ~ {u_{\ell' sj'} (r')\over {r'}^{\ell' +1}} ~ P_T (u) du$$ (63)

Using the Legendre expansion, the radial kernel function

$${\bf X}^\Lambda_{\ell L: \ell' L'} (R,R' ) = {\vert b \vert^3 \over 2} \sum_{nn'} c(\ell, n) c(\ell', n')$$

$$\times R R' (aR)^{\ell - n} (bR')^n (a' R)^{\ell' - n'} (b' R')^{n'}$$

$$\times \sum_T (2T+1) (-1)^{\Lambda+T+L+L'} ~ \hat \ell \hat \ell' ~\hat{(\ell - n)}~ \hat{(\ell' - n')} \hat n \hat {n'} \hat L \hat {L'} \nonumber$$

$$\times \sum_{K K'} (2K+1)(2K' + 1) \left ( \begin{array}{ccc}\ell - n&n'&K\\ 0&0&0 \end{array} \right )$$

$$\times \left ( \begin{array}{ccc}\ell'-n'&n&K'\\ 0&0&0 \end{arra... ...ght ) \left ( \begin{array}{ccc}K'&L'&T\\ 0&0&0 \end{array} \right ) \nonumber$$

$$\times \sum_{Q} (2Q+1) W(\ell L \ell' L' ; \Lambda Q) W(K L K' L' ; T Q)$$ (64)

$$\times \left ( \begin{array}{ccc} \ell'&Q&\ell\\ n'&K&\ell-n\\ \ell' - n'&K'&n \end{array} \right ) {\bf q}^T_ {\ell , \ell'} (R,R')$$

These formulae can also be used with ${\bf V} \equiv 1$ to calculate the kernel functions $K^\Lambda_{\ell L: \ell' L'} (R,R' )$ for the wave function overlap operators $K_{ij} \equiv\langle\Phi_i \vert\Phi_j\rangle$ needed in evaluating the non-orthogonality terms of section 8.1.

7.2.3 Zero Range Transfers

When the projectile wave functions $\varphi_\ell ({\bf r})$ are all s-states ($\ell=0$ and the interaction potential is of zero-range $({\bf V} \varphi ({\bf r}) \sim D_0 \delta ( {\bf r})~) ,$ then the form factor ${\bf X}^\Lambda_{\ell L: \ell' L'} (R,R' )$ of equation (65) can be simplified to

$${\bf X}^L_{0L: \ell' L'} (R,R') D_0 ~ {(-1)^{L' - \ell'} \over \hat L} ~ {\hat{\ell'} \hat L \hat... ...4 \pi}} ~ \left ( \begin {array}{ccc}\ell'&L &L'\\ 0&0&0\end{array} \right ) ~$$ =

$$\times {1 \over R} u_{\ell' sj'} (R ) ~ {b^2 \over a} \delta (aR+bR') .$$ (65)

This can be made local by defining a new step size $h' = -ah/b \equiv \nu_t h$ in the stripping channel $\alpha'$.

7.2.4 Local Energy Approximation

If the interaction potential is of small range, though not zero, and the projectile still contains only s-states, then a first-order correction may be made to the above form factor. This correction will depend on the rate of oscillation of the source wave function fJT (L' J'p),J' ,J't (R' ) within a `finite-range effective radius' $\rho$. The rate of oscillation is estimated from the local energy in the entrance and exit channels, and the result[12] is to multiply $u_{\ell' sj'} (R)$ in the previous section by a factor

$$\left [ 1 + \rho^2 {2 \mu _\alpha^{(p)}\over \hbar^2} ~ \left ( U... ...'} ( R) + V_{\ell' sj'} (R) -U _\alpha (R) + \epsilon _\alpha \right ) \right ]$$ (66)

where the U(R) are the optical potentials, with $V_{\ell' sj'} (r)$ the single-particle binding potential in the target. The $\mu _\alpha^{(p)}$ is the reduced mass of the particle in the projectile, and $\epsilon _\alpha$ its binding energy. At sub-Coulomb incident energies[13], the details of the nuclear potentials in equation (66) become invisible, and as the longer-ranged Coulomb potentials cancel by charge conservation, the form factor can be simplified to

$$u_{\ell' sj'} (R) \ \ D_0 \left [ 1 + \rho^2 {2 \mu _\alpha^{(p)}\over \hbar^2} \epsilon _\alpha \right ] D u_{\ell' sj'} (R)$$ = (67)

where

$$D = D_0 \left [ 1 + \left ( \rho k _\alpha^{(p)} \right ) ^2 \right ]$$ (68)

is the effective zero-range coupling constant for sub-Coulomb transfers. The parameters  D₀ and D can be derived from the details of the projectile bound state $\varphi_{0ss} ( {\bf r})$. The zero-range constant D₀ may be defined as

$$D_0 = \sqrt {4 \pi} \int_ 0^\infty r V_{0ss}(r) u_{0ss} (r) dr.$$ (69)

The parameter D, on the other hand, reflects the asymptotic strength of the wave function u_0ss (r) as $r \rightarrow \infty$, as it is the magnitude of this tail which is important in sub-Coulomb reactions:

$$u_{0ss} (r) = _ {r \rightarrow \infty} {2 \mu _\alpha^{(p)}\over \hbar^2} {1 \over \sqrt {4 \pi}} ~ D e^{-k _\alpha^{(p)} r} .$$ (70)

It may be also found, using Schrödinger's equation, from the integral

$$D = \sqrt {4 \pi} \int_ 0 ^\infty {\sinh (k^{(p)} _\alpha r)\over k^{(p)} _\alpha} ~ V_{0ss}(r) u_{0ss} (r) dr.$$ (71)

From this equation we can see that as the range of the potential becomes smaller, D approaches D₀. The `finite-range effective radius' $\rho$ of equation (68) is thus some measure of the mean radius of the potential V_0ss(r).