

Next: 4 Transition Amplitudes
Up: Methods of Direct Reaction
Previous: 2 Elimination of the
3 Model Schrödinger Equation
The Schrödinger equation for the model wave function
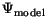 at total energy E is
at total energy E is
![$\displaystyle [E - H_{\rm opt}(E)] \Psi_{\rm model} = 0$](img58.gif) |
|
|
(14) |
We use the expansion of Eq. (1) in square-integrable states 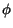 of the participating nuclei. Using for each
pair i of nuclei the `channel optical Hamiltonians' Hi defined above
(Eqs. 12 or 13), Eq. (14) becomes
of the participating nuclei. Using for each
pair i of nuclei the `channel optical Hamiltonians' Hi defined above
(Eqs. 12 or 13), Eq. (14) becomes
![$\displaystyle \sum_i^N [T_i({\bf R}_i) + V_i -E_i] \phi_{pi}\phi_{ti} \psi_i({\bf R}_i) = 0$](img60.gif) |
|
|
(15) |
where in each channel there is an asymptotic kinetic energy
Ei = E - epi-eti, corresponding
to momentum
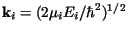 . Operating on Eq. (15) to the left
by
. Operating on Eq. (15) to the left
by
 , we obtain (after swapping the i and j indices)
, we obtain (after swapping the i and j indices)
Here, the Hamiltonian Hm in the coupling operator Vij
takes one of the forms of Eq. (13):
choosing m=i is called the post form, and choosing m=j the prior form;
the two alternatives should give the same results.
(If i and j describe different inelastic states of the same nuclei, then
 ,
we can use orthogonality of
,
we can use orthogonality of 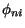 and
and 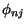 , and
the coupling Vij is just a local function of
, and
the coupling Vij is just a local function of 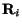 :
:
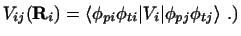 |
|
|
(17) |
This set of coupled equations (16) must be solved with boundary
conditions at large radii consisting of an incoming plane wave in channel (say)
i0, and outgoing spherical waves in all other channels:
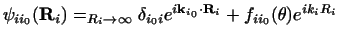 |
|
|
(18) |
Since 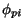 ,
, 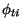 ,
, 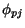 and
and 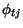 are all antisymmetrised
internally, the cross section depends on the number of identical nucleons (or nucleonic
clusters) that may be transferred in the reaction (see Austern [1, §3.5] or
Satchler[2, §2.11.3.2]). If we define npi and nti as the numbers of
nucleons (or clusters) within respectively the projectile and target states i that are
identical to the transferred set, then the scattering amplitude fii0 for each channel
i directly gives the cross section in that channel as
are all antisymmetrised
internally, the cross section depends on the number of identical nucleons (or nucleonic
clusters) that may be transferred in the reaction (see Austern [1, §3.5] or
Satchler[2, §2.11.3.2]). If we define npi and nti as the numbers of
nucleons (or clusters) within respectively the projectile and target states i that are
identical to the transferred set, then the scattering amplitude fii0 for each channel
i directly gives the cross section in that channel as
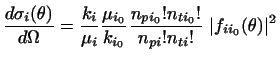 |
|
|
(19) |
(neglecting a possible elastic Coulomb amplitude in the incoming channel i0).
Partial wave expansions for the 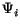 , and corresponding expressions for the
, and corresponding expressions for the
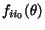 will be presented in section 6.
will be presented in section 6.


Next: 4 Transition Amplitudes
Up: Methods of Direct Reaction
Previous: 2 Elimination of the
Prof Ian Thompson
2006-02-08