5 Distorted Wave Born Approximation

Various approximate transition amplitudes may be derived by different approximations for the model wave function $\Psi_{\rm model} = \sum_i^n \phi_{pi}\phi_{ti} \psi_i({\bf R}_i)$ in the expressions (23,24,25,26). One approach is to emphasize the role of the entrance channel in the model wave function, and consider only those more direct reactions that proceed immediately from the entrance channel. Furthermore, we use in that entrance channel the wave function derived from the optical potential, not the full coupled equations (16).

5.1 One-step Born approximation

The first approximation here is to neglect the explicit calculation of multistep effects that proceed from the entrance channel i₀ via some intermediate channel(s) j to the final channel i. This will be more accurate when the intermediate channels are only weakly excited in the reaction, or when the final channel does not couple strongly to those intermediate channels that are populated. The Born approximation (BA) to the post distorted wave transition amplitude (25) is therefore

$$T_{i_0i} = \langle \phi_{pi}\phi_{ti}\chi_i^{(-)} \vert V_i-W_i \vert \phi_{p{i_0}}\phi_{t{i_0}}\psi_{i_0}^{(+)} \rangle$$ (27)

with similar one-step Born approximations to the other three transition matrix elements. These approximate DWBA forms are not invariant under the choice of distorting potential W_i, and therefore only yield useful results if this potential is chosen correctly.

5.2 Optical potential

The conventional Distorted Waves Born Approximation (DWBA) makes the second assumption that both the entrance and exit channel wave functions use the corresponding one-channel optical potentials U_i⁽¹⁾ that fitted the elastic scattering (energy-averaged in some way, if necessary). It also uses the coupling potential ${\cal V}_i$ from $V_i = U_i^{(2)} + {\cal V}_i$. The post-form and prior-form DWBA transition amplitudes, are then

$$T_{i_0i}^{\rm post DWBA} \langle \phi_{pi}\phi_{ti}\chi_i^{(-)} \vert {\cal V}_i \vert \phi_{p{i_0}}\phi_{t{i_0}}\chi_{i_0}^{(+)} \rangle$$ = (28)

$$T_{i_0i}^{\rm prior DWBA} \langle \phi_{pi}\phi_{ti}\chi_i^{(-)} \vert {\cal V}_{i_0} \vert \phi_{p{i_0}}\phi_{t{i_0}}\chi_{i_0}^{(+)} \rangle$$ = (29)

The matrix elements use optical potentials U_i⁽¹⁾ as distorting potentials which depend only on the channel radii 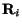${\bf R}_i$, and coupling interactions ${\cal V}_i$ will depend on coordinates of both the channels and the internal structure of the interacting nuclei. Although the prior and post DWBA expressions (28,29) are consistently equal to each other, this equality holds for any choice of distorting potentials, and does not guarantee any physical accuracy. Possible reasons for choosing different exit-channel distorting potentials W_i are discussed in §4.5 of Austern[1].