

Next: 2 Elimination of the
Up: Methods of Direct Reaction
Previous: Methods of Direct Reaction
Direct reaction theory attempts to solve the Schrödinger equation for a
specific model of the components thought to be important in a reaction, with
the component interaction potentials. In direct reaction theories, the phases describing
the superposition of all parts of the wave function are coherently maintained,
and the potentials typically include imaginary components to model how flux is
lost from the channels of the model to other channels. Direct reactions are
connected directly or via several steps with the elastic entrance channel, and
therefore have cross sections that depend on the exit angles relative to the
initial beam direction.
The intermediate states in theories of direct reactions are the discrete
states of two interacting nuclei and the relative motion of these
nuclei. These two nuclei will be the projectile and target nuclei, the
excited states of one or both of these, and those subsequent pairs of nuclei
that may be obtained by transferring one or more nucleons between them.
All the nuclei derived from the projectile will be referred to as the
`projectile-like fragment' p, and the `target-like fragment' t similarly,
with pairs of states 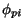 and
and 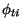 ,
and masses mpi and mti, respectively.
If these nuclei are at positions
,
and masses mpi and mti, respectively.
If these nuclei are at positions  and
and  , we form a relative
coordinate vector
, we form a relative
coordinate vector
 .
The direct reaction model space is then taken as the product of the
pairs of nuclear states and wave function
.
The direct reaction model space is then taken as the product of the
pairs of nuclear states and wave function
 for the relative
motion:
for the relative
motion:
 |
|
|
(1) |
The states can be in different mass partitions (mpi depending on
i), or they
can be different excited states of the projectile and/or the target in any
one of the partitions.
The basis states 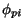 and
and 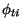 can be bound states
of their respective nuclei,
or they may be discrete representations of continuum levels.
In the former case we have a `bound state approximation',
and in the second case we have a `coupled discrete continuum channels'
(CDCC) approximation[4,5,6].
What is essential to the direct reaction framework is that they form a finite set
(N say) of square-integrable basis functions, as then we can derive a finite set of
equations coupling the channel wave functions
can be bound states
of their respective nuclei,
or they may be discrete representations of continuum levels.
In the former case we have a `bound state approximation',
and in the second case we have a `coupled discrete continuum channels'
(CDCC) approximation[4,5,6].
What is essential to the direct reaction framework is that they form a finite set
(N say) of square-integrable basis functions, as then we can derive a finite set of
equations coupling the channel wave functions
 as unknowns.
The physical Hamiltonian H contains the kinetic energy of projectile-target
relative motion
as unknowns.
The physical Hamiltonian H contains the kinetic energy of projectile-target
relative motion
 with reduced mass
with reduced mass
 , and the separate internal nuclear
Hamiltonians for the projectile- and target-like fragments are hni for
n=p, t respectively, of which the
, and the separate internal nuclear
Hamiltonians for the projectile- and target-like fragments are hni for
n=p, t respectively, of which the 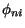 are eigenstates:
are eigenstates:
 ,
each of which is assumed to be fully
antisymmetric under the exchange of any internal pair of identical nucleons. The total
Hamiltonian H also contains the potential energy terms between the nucleons
the p and t nuclei, that couple together all the transfer and inelastic
states, whether single-particle, collective or compound.
We do not explicitly treat compound nuclear states,
where all the interacting nucleons form a single excited nucleus,
and hence all states that are produced
consequently to compound intermediate states. The effects of the compound
nuclear states will be only included in some average manner,
as described in the next section.
,
each of which is assumed to be fully
antisymmetric under the exchange of any internal pair of identical nucleons. The total
Hamiltonian H also contains the potential energy terms between the nucleons
the p and t nuclei, that couple together all the transfer and inelastic
states, whether single-particle, collective or compound.
We do not explicitly treat compound nuclear states,
where all the interacting nucleons form a single excited nucleus,
and hence all states that are produced
consequently to compound intermediate states. The effects of the compound
nuclear states will be only included in some average manner,
as described in the next section.


Next: 2 Elimination of the
Up: Methods of Direct Reaction
Previous: Methods of Direct Reaction
Prof Ian Thompson
2006-02-08
