

Next: 9 Conclusion
Up: Methods of Direct Reaction
Previous: 7 Channel couplings
Subsections
8.1 Coupled Reaction Channels
The numerical solution of Eqs. (16) is straightforward if the
inter-channel couplings Vij are local, as is the case for inelastic
excitations of one or both nuclei. These are called `coupled channels' (CC)
cases. Transfer couplings, however, couple different 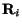 and
and 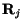 values, giving what are called `coupled reaction channels' (CRC). The
non-locality from a `finite range' treatment of recoil means that the coupled
reaction equations must be solved either iteratively, or by a R-matrix treatment
using square-integrable basis functions in an interior region. Local and
iterative solution methods are presented in ref.[3], while the
R-matrix methods presented in section 8.4, are common in atomic and
molecular scattering research, but not so widely used in nuclear scattering
problems.
A variety of standard computer programs are available for evaluation of the
couplings described above, and for solution of the coupled equations by the
methods described below. The program PTOLEMY [17] can find
coupled-channels solutions for local couplings or one-step non-local couplings
from transfers, and ECIS [15] also solves coupled-channels
equations. Both pay particular attention to the long-range couplings of Eq.
(47) that arise from inelastic Coulomb excitations. The program FRESCO [3] includes these capabilities, as well as the iterative
solutions of coupled equations with non-local couplings by all the methods to be
now described.
With non-local couplings from transfer channels, the Eqs. (16) may be
solved iteratively, and the successive iterations amount to n-th DWBA
solutions. As explained in section 3, the coupling matrix element
values, giving what are called `coupled reaction channels' (CRC). The
non-locality from a `finite range' treatment of recoil means that the coupled
reaction equations must be solved either iteratively, or by a R-matrix treatment
using square-integrable basis functions in an interior region. Local and
iterative solution methods are presented in ref.[3], while the
R-matrix methods presented in section 8.4, are common in atomic and
molecular scattering research, but not so widely used in nuclear scattering
problems.
A variety of standard computer programs are available for evaluation of the
couplings described above, and for solution of the coupled equations by the
methods described below. The program PTOLEMY [17] can find
coupled-channels solutions for local couplings or one-step non-local couplings
from transfers, and ECIS [15] also solves coupled-channels
equations. Both pay particular attention to the long-range couplings of Eq.
(47) that arise from inelastic Coulomb excitations. The program FRESCO [3] includes these capabilities, as well as the iterative
solutions of coupled equations with non-local couplings by all the methods to be
now described.
With non-local couplings from transfer channels, the Eqs. (16) may be
solved iteratively, and the successive iterations amount to n-th DWBA
solutions. As explained in section 3, the coupling matrix element
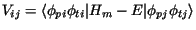 has
two different forms, depending on whether we use Hm=Hi (post form) or
Hm=Hj (prior form). If we abbreviate
has
two different forms, depending on whether we use Hm=Hi (post form) or
Hm=Hj (prior form). If we abbreviate
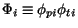 ,
these give rise to the respective matrix elements
,
these give rise to the respective matrix elements
The wave function overlap operator Kij in
equation (72) arises from the non-orthogonality between the
transfer basis states defined around different centres in
different mass partitions. We will see below that this term disappears in
first-order DWBA, and can be made to disappear in second-order DWBA, if
the first and second steps use the prior and post interactions
respectively.
If the coupling interactions Vi in Eq. (72) are
weak, or if the back coupling effects of these interactions are already
included in the optical potentials of the prior channel, then it becomes
reasonable to use a n-step distorted wave Born approximation (DWBA). This
approximation always feeds flux `forwards' in the sequence
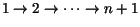 neglecting the back couplings. In
the elastic channel the wave function is governed by the optical potential
defined there, and the wave function in the i'th channel is
governed by the equation
neglecting the back couplings. In
the elastic channel the wave function is governed by the optical potential
defined there, and the wave function in the i'th channel is
governed by the equation
![$\displaystyle \left [ E_i - T_i-U_i \right ]\psi_i ( {\bf R}_i ) =
\sum _ {j=1}...
...ft\langle\Phi_i \vert {\cal H}-E \vert\Phi_j \right\rangle
\psi_j ( {\bf R}_j )$](img268.gif) |
|
|
(73) |
Initial channel:
Second channel:
![$\displaystyle \left [ E_2 - T_2-U_2 \right ]\psi_2 ( {\bf R}_2 ) =
\left\langle\Phi_2 \vert H_m-E \vert\Phi_1 \right\rangle
\psi_1 ( {\bf R}_1 )$](img270.gif) |
|
|
(74) |
If the prior interaction is used, the right hand side can be
simplified to
Final channel: c=n+1
![$\displaystyle \left [ E_c - T_c-U_c \right ]\psi_c ( {\bf R}_c ) =
\sum _ {j=1}...
...}
\left\langle\Phi_c \vert H_m-E \vert\Phi_j \right\rangle
\psi_j ( {\bf R}_j )$](img272.gif) |
|
|
(75) |
If the post interaction
had been used for all the couplings to this last channel, then
there is again a simplification:
| |
|
![$\displaystyle \left [ E_c - T_c-U_c \right ]\psi_c ( {\bf R}_c )$](img273.gif) |
|
| |
= |
![$\displaystyle \sum_ {j=1} ^ {j=c-1}
\langle\Phi_c \vert {\cal V}_c \vert\Phi_j\...
... [T_c+U_c - E_c ]~ \sum_{j=1} ^ {j=c-1}
\langle\Phi_c \vert\Phi_j\rangle \psi_j$](img274.gif) |
|
so
![$\displaystyle \left [ E_c - T_c-U_c \right ] \chi_c ( {\bf R}_c ) =
\sum_{j=1} ^ {j=c-1}
V_{nj}^{\rm post} \psi_j$](img275.gif) |
|
|
(76) |
where
Note that, as all the
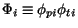 are square-integrable
and hence decay faster than r -1 at large radii,
the
are square-integrable
and hence decay faster than r -1 at large radii,
the 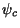 and
and 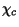 are the same asymptotically.
They differ only by an `off-shell transformation',
and hence yield the same (on-shell) scattering amplitudes.
The equation for
are the same asymptotically.
They differ only by an `off-shell transformation',
and hence yield the same (on-shell) scattering amplitudes.
The equation for 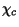 has no non-orthogonality terms once
the post interaction is used in the final channel:
this is what is meant by saying that the final channel is
`effectively on-shell'.
These results imply that in n-step DWBA, some non-orthogonality terms
can be made to
disappear if `prior' interactions are used for the first step, and/or if
`post' interactions are used for the final step. This means that the
non-orthogonality term never appears in the first-order DWBA, irrespective
of the choice of prior or post forms. In second-order DWBA, the
prior-post combination must be chosen[14]
to avoid the non-orthogonality
terms. It is clear that non-orthogonality terms will have to
be evaluated if the DWBA is continued beyond second order.
The iterative method of solving the CRC equations (16)
proceeds by analogy with the n-step DWBA iterations until the series
converges.
Convergence is readily obtained if the couplings are sufficiently small,
and different iterative strategies may be employed [17].
The procedure will however diverge if the the couplings are too large, or if
the system is too near a resonance or a bound state pole.
On divergence, the successive wave functions
has no non-orthogonality terms once
the post interaction is used in the final channel:
this is what is meant by saying that the final channel is
`effectively on-shell'.
These results imply that in n-step DWBA, some non-orthogonality terms
can be made to
disappear if `prior' interactions are used for the first step, and/or if
`post' interactions are used for the final step. This means that the
non-orthogonality term never appears in the first-order DWBA, irrespective
of the choice of prior or post forms. In second-order DWBA, the
prior-post combination must be chosen[14]
to avoid the non-orthogonality
terms. It is clear that non-orthogonality terms will have to
be evaluated if the DWBA is continued beyond second order.
The iterative method of solving the CRC equations (16)
proceeds by analogy with the n-step DWBA iterations until the series
converges.
Convergence is readily obtained if the couplings are sufficiently small,
and different iterative strategies may be employed [17].
The procedure will however diverge if the the couplings are too large, or if
the system is too near a resonance or a bound state pole.
On divergence, the successive wave functions  will become larger and larger as n increases, and not converge to
any fixed limit. Unitarity will of course be violated as the S-matrix
elements will become much larger than unity.
In this case we may use Padé approximants to accelerate the convergence of the sequence
will become larger and larger as n increases, and not converge to
any fixed limit. Unitarity will of course be violated as the S-matrix
elements will become much larger than unity.
In this case we may use Padé approximants to accelerate the convergence of the sequence
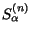 of S-matrix elements[15,17].
A given sequence
of S-matrix elements[15,17].
A given sequence
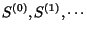 of S-matrix elements
that result from iterating the coupled equations
can be regarded as the successive partial sums of a `vector valued' polynomial
of S-matrix elements
that result from iterating the coupled equations
can be regarded as the successive partial sums of a `vector valued' polynomial
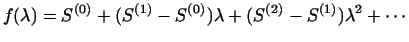 |
|
|
(77) |
evaluated at 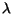 =1.
This polynomial will clearly converge for
=1.
This polynomial will clearly converge for 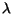 sufficiently small,
but will necessarily diverge if the analytic continuation of the
sufficiently small,
but will necessarily diverge if the analytic continuation of the
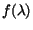 function has any pole or singularities inside the circle
function has any pole or singularities inside the circle
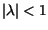 in the complex
in the complex 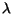 -plane.
The problem that Padé approximants solve is that of finding a computable
approximation to the analytic continuation of the
-plane.
The problem that Padé approximants solve is that of finding a computable
approximation to the analytic continuation of the 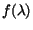 function
to
function
to 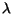 =1.
This is accomplished by finding a rational approximation
=1.
This is accomplished by finding a rational approximation
![$\displaystyle P_{[N,M]} (\lambda) = {{p_0 + p_1 \lambda + p_2 \lambda^2 + \cdot...
... \lambda^N }
\over
{1 + q_1 \lambda + q_2 \lambda^2 + \cdots + q_M \lambda^M }}$](img285.gif) |
|
|
(78) |
which agrees with the 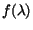 function in the region where the latter
does converge, as tested by matching the coefficients in the polynomial
expansion of
function in the region where the latter
does converge, as tested by matching the coefficients in the polynomial
expansion of
![$ P_{[N,M]} (\lambda) $](img286.gif) up to and including the coefficient of
up to and including the coefficient of
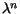 for n=N+M.
There are many different ways[18] of evaluating the coefficients
pi , qj, but for the present problem we can use
Wynn's
for n=N+M.
There are many different ways[18] of evaluating the coefficients
pi , qj, but for the present problem we can use
Wynn's 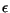 -algorithm[19,20], which is a method of evaluating
the upper right half of the Padé table at
-algorithm[19,20], which is a method of evaluating
the upper right half of the Padé table at 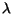 =1 directly
in terms of the original sequence
=1 directly
in terms of the original sequence
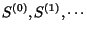 .
Experience has shown that for typical sequences the most accurate Padé
approximants are those near the diagonal of the Padé table.
We use
.
Experience has shown that for typical sequences the most accurate Padé
approximants are those near the diagonal of the Padé table.
We use
![$\overline{S^{(n)}} \equiv P_{[N,M]} (1)$](img288.gif) for N=[(n+1)/2] and M=[n/2]
in calculating the Padé-resummed cross sections.
for N=[(n+1)/2] and M=[n/2]
in calculating the Padé-resummed cross sections.
8.4 R-matrix Solutions
The radial stepping methods of solving the coupled equations only
allow local couplings to be treated properly, and non-local couplings
from transfers have to be included iteratively. The R-matrix method[21]
is an equivalent way of solving the coupled equations,
and has the advantages of being more stable numerically, and also
allowing non-local components of the Hamiltonian in an interior
region to be included to all orders. It has recently been revived in
nuclear physics applications[22,23] for these reasons.
Both transfer and non-orthogonality non-localities may be included
non-perturbatively, and resonances and bound states may be described
without difficulty.
This method uses a basis set of `energy
eigenstates' of the diagonal parts of Eqs. (34):
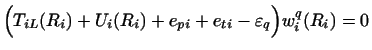 |
|
|
(79) |
for eigenenergies 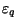 , with the basis functions all having fixed
logarithmic derivatives
, with the basis functions all having fixed
logarithmic derivatives
 at
Rm. The constancy of the logarithmic derivatives
at
Rm. The constancy of the logarithmic derivatives 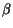 means
that (for each i channel separately) the wqi form an orthogonal basis set
over the interval [0,Rm], and over this range they can
be normalised to unity. Without this constancy, a Bloch operator must
be added to the kinetic energy to make it Hermitian.
The wave functions of the coupled problem (34) can now be
solved completely over the interior range [0,Rm], by using the
orthonormal basis set of the
{wqi(Ri)}
with coefficients to be determined. The coefficients are found in two stages:
first by finding all the eigensolutions gpi(Ri) of the
equations (34) using the above orthonormal basis, and then
expanding the scattering wave functions in terms of these gpi(Ri).
In the traditional R-matrix method, the diagonalisation of the
N-channel Hamiltonian in equation (34)
yields P=QN eigenenergies ep with corresponding multichannel eigenstates
means
that (for each i channel separately) the wqi form an orthogonal basis set
over the interval [0,Rm], and over this range they can
be normalised to unity. Without this constancy, a Bloch operator must
be added to the kinetic energy to make it Hermitian.
The wave functions of the coupled problem (34) can now be
solved completely over the interior range [0,Rm], by using the
orthonormal basis set of the
{wqi(Ri)}
with coefficients to be determined. The coefficients are found in two stages:
first by finding all the eigensolutions gpi(Ri) of the
equations (34) using the above orthonormal basis, and then
expanding the scattering wave functions in terms of these gpi(Ri).
In the traditional R-matrix method, the diagonalisation of the
N-channel Hamiltonian in equation (34)
yields P=QN eigenenergies ep with corresponding multichannel eigenstates
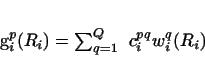 |
(80) |
Eigenstates here with ep<0 are close to the bound states, while solutions with
ep > 0 contribute to the scattering solutions. Certain of the
ep > 0 solutions may correspond to low-lying resonances if those are present,
but the majority of the positive eigenenergies have no simple physical
interpretation. These gpi(Ri) form of course another orthonormal
basis in the interior region.
For scattering states at arbitrary energy E, the coupled
solutions are then expanded in terms of the multichannel eigenstates as
 .
If we define an R-matrix at energy E by
.
If we define an R-matrix at energy E by
![\begin{displaymath}
\psi _{i}(R_i) = \sum_{i'} R_{ii'}(E)
\Bigl [ \psi{'} _{i'}(R_i) - \beta \psi _{i'}(R_i) \Bigr]
\end{displaymath}](img295.gif) |
(81) |
in the limit of
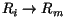 from above,
then the R-matrix
from above,
then the R-matrix 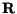 can be calculated from the
eigenstates by standard methods[21,24]
can be calculated from the
eigenstates by standard methods[21,24]
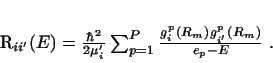 |
(82) |
The coefficients cpqi and energies ep in Eq.
(80) satisfy matrix equations
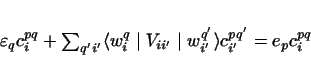 |
(83) |
for each eigenstate p, where Vii' refers to all the off-diagonal
couplings. These equations are of the matrix form
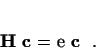 |
(84) |
There is an alternative method[25,23] for finding the Rii', which does
not diagonalise the matrix on the left side of Eq. (84), but solves a set
of linear equations.
We need the solution of
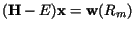 for the right
hand side consisting of the values of the basis functions at the R-matrix boundary. Then
we can solve directly
for the right
hand side consisting of the values of the basis functions at the R-matrix boundary. Then
we can solve directly
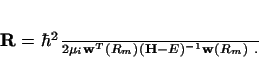 |
(85) |
This has the advantage of naturally continuing the R-matrix method to complex potentials,
avoiding the diagonalisation of non-Hermitian matrices.
Using Eqs. (36) and (81), and writing the Coulomb
functions 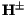 as diagonal matrices, the scattering S-matrix is given
in terms of
as diagonal matrices, the scattering S-matrix is given
in terms of 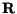 by
by
![\begin{displaymath}
{\bf S} = [{\bf H^+}\! -\! {\bf R}({\bf H'^+}\! -\! \beta ...
...[ {\bf H^-}\! -\! {\bf R}({\bf H'^-}\! -\! \beta {\bf H^-}) ]
\end{displaymath}](img304.gif) |
(86) |
and the expansion coefficients for the wave functions are
The R-matrix calculated by Eq. (82) is only exact when the
sum over p extends to all energies ep. To improve the accuracy of
calculations with finite Q (and hence finite P), the Buttle
correction[26] is added to the right hand side of
Eqs. (82,85).
This modifies the diagonal terms Rii(E)
to reproduce for each uncoupled problem the exact scattering solution 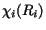 after this has been integrated separately.
From the definition of the energy eigenstates wqi(Ri), the
R-matrix sum from (82) for each uncoupled channel is
after this has been integrated separately.
From the definition of the energy eigenstates wqi(Ri), the
R-matrix sum from (82) for each uncoupled channel is
 |
(88) |
and the exact one-channel R-matrix is
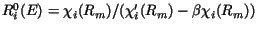 .
The Buttle-corrected full R-matrix to be used in Eq. (86) is then
.
The Buttle-corrected full R-matrix to be used in Eq. (86) is then
![\begin{displaymath}
R^c_{ii'}(E) = R_{ii'}(E) +
\delta_{ii'}
\Bigl [~ R^0_{i}(\tilde E) - R^u_{i}(\tilde E)\Bigr ] \ .
\end{displaymath}](img311.gif) |
(89) |
The energy 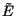 can be equal to E, or chosen just near to it if necessary
to avoid the poles in Eq. (88), since the Buttle correction varies
smoothly with energy.
The solution of the CRC equations (16) with all the non-orthogonality terms
in Eq. (72) requires in Eq. (83) the matrix element integrals of the form
can be equal to E, or chosen just near to it if necessary
to avoid the poles in Eq. (88), since the Buttle correction varies
smoothly with energy.
The solution of the CRC equations (16) with all the non-orthogonality terms
in Eq. (72) requires in Eq. (83) the matrix element integrals of the form
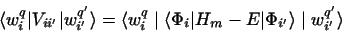 |
(90) |
for m=i (post) or m=i' (prior).
In the post form, Hm contains Ti+Ui, and since wqi is just the eigenfunction of
this operator with eigenvalue 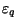 , we can operate to the left to obtain
, we can operate to the left to obtain
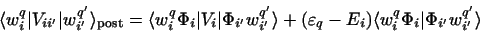 |
(91) |
with the similar prior form
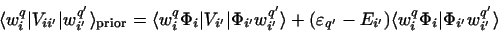 |
(92) |
The wave function overlaps in the second term
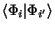 go to zero asymptotically, and may be assumed small when Ri, Ri'>Rm.
The standard R-matrix theory therefore still applies in the asymptotic region.
go to zero asymptotically, and may be assumed small when Ri, Ri'>Rm.
The standard R-matrix theory therefore still applies in the asymptotic region.


Next: 9 Conclusion
Up: Methods of Direct Reaction
Previous: 7 Channel couplings
Prof Ian Thompson
2006-02-08
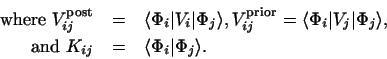
![$\displaystyle \left [ E_i - T_i-U_i \right ]\psi_i ( {\bf R}_i ) =
\sum _ {j=1}...
...ft\langle\Phi_i \vert {\cal H}-E \vert\Phi_j \right\rangle
\psi_j ( {\bf R}_j )$](img268.gif)
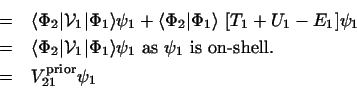
![$\displaystyle \left [ E_c - T_c-U_c \right ]\psi_c ( {\bf R}_c ) =
\sum _ {j=1}...
...}
\left\langle\Phi_c \vert H_m-E \vert\Phi_j \right\rangle
\psi_j ( {\bf R}_j )$](img272.gif)
![$\displaystyle \sum_ {j=1} ^ {j=c-1}
\langle\Phi_c \vert {\cal V}_c \vert\Phi_j\...
... [T_c+U_c - E_c ]~ \sum_{j=1} ^ {j=c-1}
\langle\Phi_c \vert\Phi_j\rangle \psi_j$](img274.gif)
![$\displaystyle \left [ E_c - T_c-U_c \right ] \chi_c ( {\bf R}_c ) =
\sum_{j=1} ^ {j=c-1}
V_{nj}^{\rm post} \psi_j$](img275.gif)

![$\displaystyle P_{[N,M]} (\lambda) = {{p_0 + p_1 \lambda + p_2 \lambda^2 + \cdot...
... \lambda^N }
\over
{1 + q_1 \lambda + q_2 \lambda^2 + \cdots + q_M \lambda^M }}$](img285.gif)
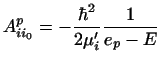
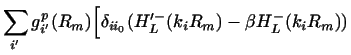
![$\displaystyle - S_{ii_0}
(H'^+_L(k_iR_m)-\beta H^+_L(k_iR_m))
\Bigr ] \ .$](img307.gif)