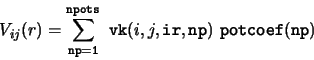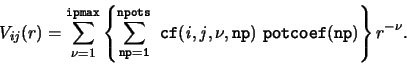4 File Specifications

Here, the notation (R;*) means a real variable with free format input

FILE fpot.spec

title(1)

(S;a80) Descriptive information for echoing to standard output

ryev,coulcn

(R,R;*)
Values of $\hbar^2/2m$ and e²

roin,rostep,nrooo,ppr0,ppdr,nrpp,rinner

(R,R,I,R,R,I,R;*)
Coupling potentials in mel file give at nrooo radial points starting at roin and then with steps of rostep.
Forbidden states in occ file give at nrpp radial points starting at ppr0 and then with steps of ppdr. Define rppmax = (nrpp-1)*ppdr+ppr0.
The forbidden states are assumed to form an orthonormal set up to radius rinner: rmax should be greater than or equal to rinner = rppmax.

nbody,scent,lxtra,ncoup,ipmax,mfad,symm,details,npots,mstates,nmoms

(I,R,4*I,L,L,3*I;*)
nbody = A, the number of bodies, and
scent = $\Delta$ (usually (3A-6)/2).
lxtra = no. of quantum numbers in the set $\gamma$.
ncoup = no. of specifications of coupling orders.
ipmax=$\Lambda+1$, the maximum inverse power in asymptotic region.
mfad = number of Faddeev components.
symm if couplings symmetric.
details if details of the A bodies to be read below.
npots = number of potential sets in the mel file.
mstates = upper bound to all the npstates(:) values below.
nmoms = number of moment-matrices to read from mel file.

qnum(1:lxtra+1)

(S;30a3)
Names of the quantum numbers, beginning with qnum(1)='K' or 'L'.
For nbody=2, the spbe transition subroutine assumes
the coupling order L, 2*s, 2*j, 2*I with lxtra$\geq$3;
For nbody=3, the belmag, conasf, conden and consf transition subroutines assume
the coupling order K, L, S, L1, L2, Jn, 2*I, 2*S1, 2*S2, J with lxtra$\geq$6.

mult(1:lxtra+1),jgt

(I;30i3) Multiplying factors (1 or 2) for quantum numbers to be integer.
jgt = index to quantum number of total spin.

((cupord(i,j),i=1,3),j=1,ncoup)

(I;20i3)
For each coupling order a+b = c, the indices of quantum nunbers a, b and c.

If details:

 

mass(nbody),charge(nbody),radius(nbody)

(R;*)
Masses, charges and point-nucleon radii of the nbody bodies.
Next line repeated for ib=1,nbody:

(name(ib),npstates(ib),corek(ib),Qmom(ib),Mmom(ib),

 
(energy(i,ib),nparity(i,ib),i=1,npstates(ib))
(S,I,3*R, (R,I); a8,i3, f4.1,2f10.4, 10(f8.4,i4))
For each body, give its name, number of states, K-projection for any rotational model, intrinsic quadrupole moment Q₀, magnetic moment. Then, for each state, give excitation energy and parity.

(id(i),iso(i),i=1,npair)

((L,R);*)
For npair = nbody*(nbody-1)/2 possible pairs of bodies, if id, the isospin state iso.

((nucl(j,i),j=1,nbody),i=1,mfad)

(R;*)
For each of the mfad Faddeev components, the ib index that ichl (later) will refer to.

Remaining lines repeated until end of file for each $J^\pi$ set:

 

title(2)

(S;a80) Descriptive information for each 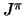$J^\pi$ set

jj2,npty,nchan,mintl,xla,escatt

(4*I,R,R; 4i5,f10.5,e12.4)
2J, parity (+1 or -1), number of channels nchan, any potential variation parameter xla.
mintl=number of elastic channels.
escatt=scattering energy (c.m.) to, if non-zero, override ebeg etc.

If details:

(kfad(i),i=1,nchan)

(I,*) Number of Faddeev component (1..mfad) for each channel.

If details: Next line for ib=1,nbody:

(ichl(i,IB),i=1,nchan)

(I,*) Index to states of each body in each channel.

(lchl(i),i=1,nchan)

(I,*)
Orbital angular momentum K. The centrifugal barrier will use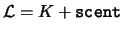 ${\cal L} = K + {\tt scent}$.

Next line for ix=1,lxtra:

(lxtr(ix,i),i=1,nchan)

(I,*)
Extra quantum numbers in the set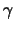 $\gamma$, multiplied by mult(ix+1) so as to be integers.

Next line if mintl>0:

(initl(i),i=1,mintl)

(I,*)
Numbers of the mintl elastic channels for output to file 73 in FRESCO format.

nsrc,nkill

(I,I;*)
nsrc = number of forbidden-state projection operators in occ file.
If nsrc < 0, assume compact format in the occ file (see below).
nkill = number of Pauli-forbidden energy surfaces (not implemented).

FILE fpot.mel (binary: real*8)

If symm:

 
For I1=1,nchan, For I2=I1,nchan, For np=1,npots,
    read (vk(I1,I2,ir,np),ir=1,nrooo), (cf(I1,I2,ip,np),ip=1,ipmax)

If not symm:

 
For I1=1,nchan, For I2=1,nchan, For np=1,npots,
    read (vk(I1,I2,ir,np),ir=1,nrooo), (cf(I1,I2,ip,np),ip=1,ipmax)

For I1=1,nchan, read (wn1(I1,I2),I2=1,nchan)
read (mp12(I2),I2=1,nchan)

All cases:

 
For im=1,nmom, for I1=1,nchan,
read (moms(I1,I2,im),I2=1,nchan)

This file gives the coupling potentials, for $r = {\tt roin+(ir-1)*rostep}$,

$$V_{ij}(r) = \sum_{\tt np=1}^{\tt npots} ~ {\tt vk}(i,j,{\tt ir,np) ~ potcoef(np)}$$ (52)

up to the radius roin+(nrooo-1)*rostep. Beyond this point, the couplings are found from the asymptotic expansion

$$V_{ij}(r) = \sum_{\nu=1}^{\tt ipmax} \left \{ \sum_{\tt np=1... ...~ {\tt cf({\it i,j},\nu,np) ~ potcoef(np)} \right \} r^{-\nu}.$$ (53)

Any Coulomb potentials must be explicitly included in the vk values, and as $\nu$=1 terms in the asymptotic expansions. Off-diagonal Coulomb monopoles are ignored.

The moms(i,j,im) arrays contains the matrix elements of the im=1,nmom moments to be evaluated for all examined bound states.

FILE fpot.occ (binary: real*8, default integer)

The |nsrc| forbidden states $\{ \tilde{w}_{mn}\}$ of eqn. (19) are read in:

If nsrc > 0:

 
read ((WFfor(i,j),j=1,nrpp),i=1,nchan)

If nsrc < 0:

 
read MCHP,jmin,jmax,(chans(i),i=1,MCHP), ((WFfor(chans(i),j),j=jmin,jmax),i=1,MCHP)
Read the number of non-zero channels MCHP, the minimum and maximum radial indices jmin,jmax, the channel numbers chans of these, and then the forbidden state wave functions. The other channels are set to zero.

and used to make projection operator P by eqn. (19). The forbidden states are assumed to be orthogonal, but they are renormalised to unity in the basis used in sturmxx.

List of all output and temporary files

file number	Use	In subroutine:
1	Buttle corrections	BASIS or RMATRIX
2	Trace	BASIS etc
3	Trace information	XLR (many routines)
4	Misc output	BELMAG,CONSF,BASIS etc
5,6	STANDARD INPUT, OUTPUT	many places
8	Scattering wave functions	SCATTERING
9	Diagonal scattering wave functions	SCATTERING
10	B(E1) output cross sections	BELMAG
11	gs wave functions	PROBABILITY
12	READ matrix elements (mel)	READCC
13	READ channel specifications (spec)	READCC
14	READ orthogonality conditions (occ)	READCC
15	Eigenenergies of internal Hamiltonian	PROBABILITY
17	B(E1) discretised output	BELMAG
19	gs+scatt wave functions (binary)	SCATTERING
20	READ gs expansion coefficients (binary)	STURMHH
21	gs expansion coefficients (binary)	STURMHH
22	All expansion coefficients	PROBABILITY
23	Norms of internal eigenstates	ENORM
24	B(I0)	BELMAG
25	Summed strength functions	CONASF
26	Norms of internal eigenstates	ENORM
27	Scattering phases	TMAT and TMATP
28	Strength functions	CONSF
29	Eigenphases	TMATT
30	Interior norms	SCATTER
31	Buttle corrections	BASIS or RMATRIX
32	B(I0) discrete	BELMAG
33	Buttle corrections	BASIS or RMATRIX
36	READ Average sturmian potential	BASIS
37	Average probabilities of sturmians	PROBABILITY
38	Average sturmian potential	PROBABILITY
40	Sturmian potential used	BASIS
41	Eigenpotentials	BASIS
43	Determinants in gs search	BOUND
44	Wronskian errors	WRONSK in XLR
48	gs wave function (binary)	PROBABILITY
49	Forbidden state norms	MAKEMAT
50+l	B(El) responses	SPBE
60	Propagated wfns	LWFPRP
69	Wronskian errors in bs wfns	LWFPRP
idiscr = 71	LW diagonalisations	SLWPOT (scratch)
idiscr+1 = 72	Global propagators	LWFPRPO (scratch)
73	S-matrix elements (binary)	TMAT
77	READ gs wave function	READCC
78	Save gs wave function	PROBABILITY
79	Wronskian errors, R-matrix norm	ASYMS
80+i	Valence Strength functions for i=LSJ	CONASF
92	E1 transition integrands	BELMAG
105,106	External wave functions (real,imag)	ASYMO
110	B(E1) output amplitudes	BELMAG
111,112	External wave functions (real,imag)	SCATTERING
117	B(E1) discretised amplitudes	BELMAG

file number	Use	In subroutine:
118	Non-real energy surfaces	SLWPOT/VDIAG
120	Adiabatic energy surfaces	SLWPOT/VDIAG
121	Adiabatic energy surfaces *r2	SLWPOT/VDIAG
128	k/tan(Scattering phases)	TMAT and TMATP
150	R-matrix & Buttle parameters	SCATTERING
152	Coefficients of asymptotic wfn for gs	BNDBS
153	Log10 of asymptotic wfn for gs	BNDBS
158	Valence transition amplitudes	CONASF
159	Core transition amplitudes	CONACSF
160+c	Wave functions of basis states in ch. c	BASIS
170+i	Integrated transition densities	CONDEN
180+i	Transition densities for i=LSJ	CONDEN
190+i	Core Integrated transition densities	CONDEN
200+i	Core Transition densities for i=LSJ	CONDEN
210	Summed Core Strength functions	CONACSF
210+i	Core Strength functions for i=LSJ	CONACSF
nftt	T-matrix (binary)	TMATT,TMATP