Card for text describing run.
Name of file stem: to create FPOT.mout with additional output, and (if NMAX=0) FPOT.spec, FPOT.mel and FPOT.occ with files for STURM.
- AC
- mass of core nucleus
- ZC
- charge of core nucleus
- RCORE
- r.m.s. matter radius of target nucleus
- NTARG
- abs(NTARG) = number of target states
If NTARG < 0, then the VOLCON logical variable is set TRUE for use by the potential function routines UC(L,R) etc. and read:- (DEFH(I),I=2,5)
- Deformation lengths for 3-body Hamiltonian, as DEF only used for occupied states.
- KTARG
- K projection for coupling states by the rotational model (real)
- DEF(2:5)
- deformation lengths
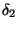 ,
, 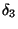 ,
, 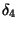 ,
and
,
and 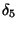 . These deformation lengths are found
from the fractional deformations
. These deformation lengths are found
from the fractional deformations 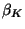 by
by
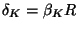 for nuclear radius R.
for nuclear radius R.
- JTARG
- spin Jc (real)
- PTARG
- parity
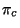 (integer +1 or -1)
(integer +1 or -1)
- ETARG
- energy Ec
- Q0CORE
- Intrinsic quadrupole moment of core, used for E2 transitions.
- AN
- mass of valence particle
- ZN
- charge of valence particle
- RN
- r.m.s. matter radius of valence particle (0 for nucleons!)
- SN
- spin s of valence particle, 0 or 0.5 (real)
- TT
- isospin of valence particle, 0 or 1 (integer)
- ZN2
- charge of second valence particle (read in if ZN>0)
- RSCR
- screening radius for Coulomb potentials (RSCR=0 is no screening) (read in if ZN>0)
- H2M
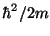 for unit mass m. Use 20.900795 for AC, AN in amu,
and 20.721 for masses in units of neutron mass. With neutron mass units, use
20.748 for the old HH programs and 20.735 for the old CSF programs.
for unit mass m. Use 20.900795 for AC, AN in amu,
and 20.721 for masses in units of neutron mass. With neutron mass units, use
20.748 for the old HH programs and 20.735 for the old CSF programs.
- KMAX
- Max. hyperharmonic K
- LNCMAX
- Max. angular momentum Lcn (between core and neutron) with non-zero potential
- LNNMAX
- Max. angular momentum Lnn (between two neutrons) with non-zero potential
- SMAX
- Max. spin S of the two neutrons (integer 0 or 1)
- LLMAX
- Max. angular momentum L = Lcn + Lnn
- L2MX
- Absolute value is max. angular momentum
 between
the interacting pairand the spectator.
between
the interacting pairand the spectator.
- EQN
- (character in quotes) Type of equation to solve:
'F'=Faddeev, 'T'=T-Schrodinger:HH, 'Y'=Y-Schrodinger.
If 'a' lle EQN lle 'z', then set FESH=true for Feshbach reduction. - JNNMX(1:-L2MX)
- Max. angular momentum Jnn of valence pair, for each L (i.e. read only if L2MX<-1).
Max. hyperharmonic K for each particular L=Lnn and IC, followed by max. K for both
This card is repeated for each IC=1 to NTARG.
Max. hyperharmonic K for each particular L=Lcn and IC, followed by max. K for both
This card is repeated for each IC=1 to NTARG.
- PWFILE
- (string in quotes) name of file of partial wave weights from previous calculation.
- THRESH
- real positive threshold for including partial waves in this calculation.
- Kmaxf(1:NTARG)
- Perform Feshbach reduction to
 for each
target state.
for each
target state.
- EFesh
- Feshbach target eigenenergy
- RLOC
- Radius for local Pauli blocking
- NDROP
- Number of adiabatic energy surfaces to drop for Pauli Blocking.
- RR
- Scaling factor for hyperradius grid
- NLAG
- Number of hyperradial grid points.
If NMAX 0, use NLAG Gauss-Laguerre quadrature points, and perform
diagonalisation for eigen-energies
0, use NLAG Gauss-Laguerre quadrature points, and perform
diagonalisation for eigen-energies
If NMAX = 0, use NLAG regularly spaced hyperradial points from RR to RR*NLAG, and write the output files FPOT.spec, FPOT.mel and FPOT.occ with files for STURM - NJAC
- Number of Gauss-Jacobi hyperangular quadrature points.
- RINNER
- Radius for orthonormalisation of Pauli Projection operators
- NJT
- Number of angular momentum/parity sets (integer)
- JTOTS(i)
- Total angular momentum (real)
- PARITIES(i)
- (character in quotes) Parity ('+' or '-')
- NJT,JTOTS,PARITIES
- As above
- DROPS
- Number of adiabatic energy surfaces to drop for Pauli Blocking for each spin/parity combination given.
- NMAX
- Number of Legendre-polynomial basis functions for diagonalisation.
If NMAX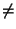 0, use NLAG Gauss-Laguerre quadrature points, and perform
diagonalisation for eigen-energies
0, use NLAG Gauss-Laguerre quadrature points, and perform
diagonalisation for eigen-energies
If NMAX = 0, use NLAG regularly spaced hyperradial points from RR to RR*NLAG, and write the output files FPOT.spec, FPOT.mel and FPOT.occ with files for STURMXX - EMIN
- If NMAX > 0, energy for inverse iteration: find eigenstates
nearest to EMIN. Find MEIGS states.
If NMAX < 0, find all eigensolutions. MEIGS must be large enough. - DE
- (Read if NMAX<0) Energy step for discrete response functions.
- EMAX
- (Read if NMAX<0) Maximum energy for discrete response functions.
- MEIGS
- Number of eigensolutions to find.
- MOMDIS
- For each solution calculate the spherical & projected momentum momentum distributions, using momentum up to kmax = 2 fm-1.
- DX
- step size for bound states
- XMAX
- max. radius for bound state wave functions.
- DY
- spacing of splines for y dimension of each blocked state
- YMAX
- maximum y of each spline set.
- RNODE
- max. radius for counting nodes in bound state wave functions.
- ITRBS
- Non-zero to print bound state details (e.g. odd for wave functions).
- LBSMAX
- Maximum l for bound-state wave functions.
- KAPP
- Non-linearity parameter for spline functions in Pauli blocking (if zero, use 1d-3)
- EPS2
- {read if KAPP<0}: threshold norm of Pauli projection operators, (default value is 0.1)
- N3BLOCK
- {read if KAPP<0}: number of 3-body bound states to read in 51, to give blocking projection operators (default value is zero).
Occupied Y states
or occupied T states
card repeated until the following line of zeros is read.
- BKIND
- Component kind: 1 for
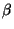 (nucleon-core=Y),
2 for
(nucleon-core=Y),
2 for 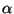 (NN=T) occupied states.
(NN=T) occupied states.
BKIND=3 or 4 (resp.) for transfer states.
BKIND=5 or 6 (resp.) for continuum bin states (unoccupied!).
If BKIND < 0, use |BKIND| as a test wavefunction only (not occupied).
If BKIND > 10, then use BKIND-10 (and BKIND+10 if BKIND<-10) and also, if searching for potential scaling factor, save this factor in array VSCALE(mod(l,2)) for use by potential function UC(L,R) for e.g. rescaling the central potential to depend on the parity of the ground state. Also read in DE,NK,ISC - NV
- Number n of nodes (including origin) in first component with
l = LV (except if NOM < 0).
If NV < 0, force unbound state search.
For continuum bins, the incoming channel is number NV. - LV
- An l value in the bound state:
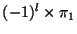 gives overall parity
gives overall parity
- JV
- BKIND=1,3: Total angular momentum J in state
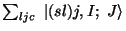 (real)
(real)
BKIND=2,4: Total angular momentum J in state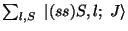 (real)
(real)
- BE
- If positive, use this binding energy, and rescale the potential;
if zero, find binding energy for fixed potential;
if negative, search for unbound state giving phase shift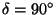 .
.
- START
- Initial value for binding energy or potential multiplier
- NOM
- If NOM < 0,
make NV the number of nodes in channel number |NOM|,
and ensure that this channel is non-zero.
If NOM > 0, read in list of omitted partial waves:
one per new card in format (integer, real, integer): l, j, c (c = core state index).
- If BKIND=5 or 6
- Also read a card with:
- DE
- Width of bin in MeV: from |BE|-DE/2 to |BE|+DE/2
- NK
- Number of k values in quadrature for bin.
- ISC
- Scaling weight factor before quadrature:
2: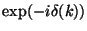 4:
4:
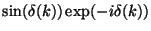 12:
12:
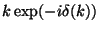 14:
14: