NN and NC potentials

These are specified by including FORTRAN functions for:

NN interaction: VC(L,R), VLS(L,R), VT(L,R), VLL(L,R) where VLS is the ${\bf (s_{n1} + s_{n2}) \cdot L}$ interaction;

NC interaction: UC(L,R), ULS(L,R), ULSC(L,R), ULL(L,R), UT(L,R) where ULS is the neutron spin-orbit ${\bf s_n \cdot L}$ and ULSC the core spin-orbit ${\bf J_c \cdot L}$ potential.

VT and UT are tensor potentials using spins ${\bf (s_{n1} + s_{n2})}$ and ${\bf (s_{n} + J_c)}$ respectively, and do not change the core state ${\bf J_c}$.

When any $\delta_K \ne 0$, the central interaction UC(L,R) is deformed by all the non-zero $\delta_K$ according to

$$V_{\tt L}(r,\theta) = {\tt uc}({\tt L},r - \sum_{K=2}^5 \delta_K P_K(\cos \theta) \sqrt{\frac{2K+1}{4\pi}})$$

and projected by 9-point Gaussian quadrature onto K=0 and those multipoles $K\ge2$ for which $\delta_K \ne 0$. The resulting $V_{\tt L}^K(r)$ are used to to couple core states $J_c,J_c^\prime$ for which $\Delta(J_c,J_c^\prime,K)$ holds, according to a collective model. The value of L is given by the angular momentum between the particle and the core in the partial wave being fed by the interaction.

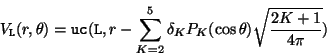
If all the JTARG values are zero, then the quadropole deformation length is used to construct a form factor for monopole excitation couplings.

NC interaction outside RINNER: UUC(L,R), UULS(L,R) replace UC and ULS.

Three-body interaction: V3B(RHO,...), U3B(RHO,...) for NN and NC partitions respectively.