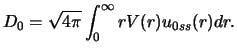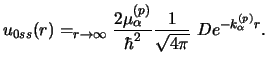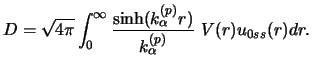

Next: 5 Numerical Solutions
Up: Coupled Reaction Channels Calculations
Previous: 3 Wave Functions for
Subsections
4 Coupling Interactions
When two nuclei interact, a variety of kinds of elastic and inelastic
potentials may be needed to describe their interaction.
As well as the scalar nuclear attractions and scalar Coulomb repulsions,
if either of the nuclei has spin  , then there can be
higher-order tensor interactions which couple together the spin and the
orbital motion. If a nucleus has spin
, then there can be
higher-order tensor interactions which couple together the spin and the
orbital motion. If a nucleus has spin
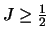 , then there can be
a spin-orbit component
, then there can be
a spin-orbit component
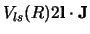 in the
Hamiltonian
in the
Hamiltonian 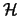 . and if its spin is one or greater
(
. and if its spin is one or greater
(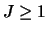 ), there can be tensor forces of various kinds.
The most commonly used tensor force is a Tr potential
of the form
), there can be tensor forces of various kinds.
The most commonly used tensor force is a Tr potential
of the form
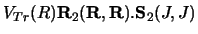 .
Similar tensor forces are also generated if the projectile and target
spins coupled together can reach
.
Similar tensor forces are also generated if the projectile and target
spins coupled together can reach
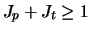 :
such is the case with the tensor force between the proton and the neutron
within the deuteron.
:
such is the case with the tensor force between the proton and the neutron
within the deuteron.
Inelastic potentials (4.2) arise when one or both of the
nuclei have permanent deformations (as seen in their intrinsic frame),
or are vibrationally deformable. The inelastic potentials which come from
rotating a permanently deformed nucleus are described in the Hamiltonian
by terms of the form
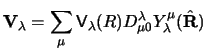 |
|
|
(70) |
where the form factors
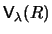 have both nuclear and
Coulomb components for angular momentum transfers
have both nuclear and
Coulomb components for angular momentum transfers 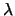 .
Their nuclear component is approximately proportional
to the derivative of the scalar potential between the two reaction
partners. Simultaneous excitations of both nuclei are also possible
(see e.g. [17]), but have not been included in the present code.
Vibrational excitations of a nucleus have more complicated form factors in
general [1], but can still be expanded in the form of
equation (70).
For the more intricate level schemes of strongly-deformed nuclei, it will
in general be necessary for each allowed transition to have its own
transition rate specified independently of a particular rotational or
vibrational model.
.
Their nuclear component is approximately proportional
to the derivative of the scalar potential between the two reaction
partners. Simultaneous excitations of both nuclei are also possible
(see e.g. [17]), but have not been included in the present code.
Vibrational excitations of a nucleus have more complicated form factors in
general [1], but can still be expanded in the form of
equation (70).
For the more intricate level schemes of strongly-deformed nuclei, it will
in general be necessary for each allowed transition to have its own
transition rate specified independently of a particular rotational or
vibrational model.
Inelastic potentials also arise when one of the
nuclei can be decomposed into a `core' + `valence particle'
structure 4.3),
such that the opposing nucleus interacts with the two
components with distinct potentials acting on distinct centres-of-mass.
The valence particle can be a single nucleon, as in the case of
17O = 16O + n, or it can be a cluster of nucleons,
as in 6Li = + 2H, or
7Li =
+ 2H, or
7Li = + 3H. In all these cases, there arise
inelastic potentials which can re-orient the ground state of the
composite nucleus, or can excite the valence particle into higher-energy
eigenstates.
+ 3H. In all these cases, there arise
inelastic potentials which can re-orient the ground state of the
composite nucleus, or can excite the valence particle into higher-energy
eigenstates.
Finally, transfer interactions (4.4) arise when the
reaction brings about the transfer of a valence particle from one nucleus
into a bound state around the other. As the incoming and outgoing
projectiles have different centres-of-mass, with the targets likewise,
the correct treatment of transfer interactions requires taking into
account the effects of recoil and of the finite ranges of the binding
potentials. These result in the coupling form factors becoming non-local,
so that they must be specified by the two-dimensional kernel functions
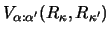 in equation (30). They also require that the coupled equations be solved
by iteration, as will be discussed in section 5.
If the effects of recoil are neglected, the `no-recoil' (NR)
approximation is obtained, but in general[72]
this is inaccurate in ways which are difficult to predict. For that reason
the NR approximation is not included in the present code.
For many light-ion reactions, however, another `zero-range'
approximation is available, and this does remove many of the finite-range
requirements. Alternatively, a first-order correction for the finite-range
effects may be estimated, to give the `local energy approximation'.
These two special cases are discussed at the end of the section.
in equation (30). They also require that the coupled equations be solved
by iteration, as will be discussed in section 5.
If the effects of recoil are neglected, the `no-recoil' (NR)
approximation is obtained, but in general[72]
this is inaccurate in ways which are difficult to predict. For that reason
the NR approximation is not included in the present code.
For many light-ion reactions, however, another `zero-range'
approximation is available, and this does remove many of the finite-range
requirements. Alternatively, a first-order correction for the finite-range
effects may be estimated, to give the `local energy approximation'.
These two special cases are discussed at the end of the section.
This section presents the matrix elements for spin-orbit forces and a
variety of tensor interactions. The radial form factors
 which multiply these matrix elements are not
specified, since these are usually determined by a fitting procedure
in an optical-model search code, and a wide variety of
parameterised forms have been used.
which multiply these matrix elements are not
specified, since these are usually determined by a fitting procedure
in an optical-model search code, and a wide variety of
parameterised forms have been used.
We shall use the
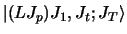 representation
for the order of coupling the spins, as in equation (24).
representation
for the order of coupling the spins, as in equation (24).
For the projectile spin-orbit force
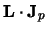
| |
|
 |
|
| |
|
![$\displaystyle = \delta_{L L'} \delta_{ J_1 J'_1 }
\frac{1}{2}[ J_1 ( J_1 +1) - L(L+1) - J_p( J_p+ 1) ]$](img261.gif) |
(71) |
This convention amounts to a
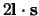 spin-orbit force, rather
than one based on
spin-orbit force, rather
than one based on
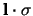 . These are the same for nucleons
and spin
. These are the same for nucleons
and spin  nuclei, but it means, for example, that the
spin-orbit strengths for deuterons and 7Li will
have to be decreased as they have
nuclei, but it means, for example, that the
spin-orbit strengths for deuterons and 7Li will
have to be decreased as they have  = 1 and 3/2 respectively.
= 1 and 3/2 respectively.
For the target spin-orbit interaction
 , we first transform
, we first transform
so
We use the notations of ref. [18]:
 |
|
|
(73) |
and
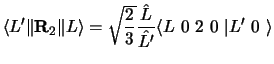 |
|
|
(74) |
for the reduced matrix elements of the second-rank spin and radial tensors
respectively.
With the projectile 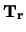 tensor force
tensor force
 ,
the coupling interactions are
,
the coupling interactions are
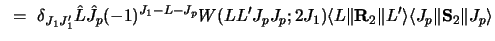 |
|
|
(75) |
For the target 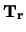 tensor force
tensor force
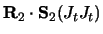 the coupling interactions are
the coupling interactions are
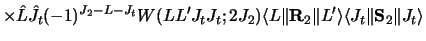 |
|
|
(76) |
For the combined target-projectile 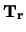 tensor force
tensor force
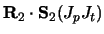 the coupling interactions are
the coupling interactions are
 |
|
|
(77) |
where the second-rank reduced matrix element is
Consider a deformed nucleus with deformation lengths
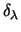 .
The effect of these deformations can be expressed as a change in the radius
at which we evaluate the optical potentials, the change depending on the
relative orientations of the radius vector to the intrinsic orientation
of the nucleus. Deformation lengths are used to specify the these
changes, rather than fractional deformations
.
The effect of these deformations can be expressed as a change in the radius
at which we evaluate the optical potentials, the change depending on the
relative orientations of the radius vector to the intrinsic orientation
of the nucleus. Deformation lengths are used to specify the these
changes, rather than fractional deformations  ,
to remove a dependence on the `average potential radius'
RU. This is desirable because often the real and imaginary
parts of the potential have different radii, and it is not clear which is
to be used. It also removes a dependence on exactly how the `average
radius' of a potential is to be defined.
,
to remove a dependence on the `average potential radius'
RU. This is desirable because often the real and imaginary
parts of the potential have different radii, and it is not clear which is
to be used. It also removes a dependence on exactly how the `average
radius' of a potential is to be defined.
When U(R) is the potential shape to be deformed,
the coupling interaction is
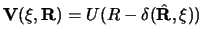 |
|
|
(78) |
where the `shift function' has the multipole expansion
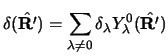 |
|
|
(79) |
(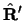 is the vector
is the vector 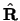 in the
body-centred frame of coordinates defined by
in the
body-centred frame of coordinates defined by 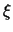 ).
Transforming to the space-fixed frame of reference,
and projecting onto the spherical harmonics,
the multipole expansion becomes
).
Transforming to the space-fixed frame of reference,
and projecting onto the spherical harmonics,
the multipole expansion becomes
The correction 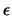 is designed ([45])
to ensure that the volume integral of the monopole potential
is designed ([45])
to ensure that the volume integral of the monopole potential
 is the same as that of U(R), and is correct
to second order in the
is the same as that of U(R), and is correct
to second order in the
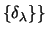 .
.
When the
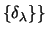 are small, the above multipole functions
are simply the first derivatives of the U(R) function:
are small, the above multipole functions
are simply the first derivatives of the U(R) function:
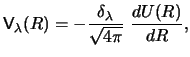 |
|
|
(84) |
with the same shape for all multipoles  .
.
The deformations of the Coulomb potential can also be defined by the
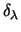 , but unfortunately an average potential radius is
again introduced. The dependence on models for average radii can be
reduced by defining the Coulomb deformations in terms of a reduced matrix
element such as that of Brink and Satchler [19], or that of Alder and Winther
[20].
For the present purposes we adopt that of Alder and Winther, as it is
hermitian upon interchanging the forward and reverse directions.
We include, however,
a simple phase factor to keep it real-valued. The new deformation
parameter is called
, but unfortunately an average potential radius is
again introduced. The dependence on models for average radii can be
reduced by defining the Coulomb deformations in terms of a reduced matrix
element such as that of Brink and Satchler [19], or that of Alder and Winther
[20].
For the present purposes we adopt that of Alder and Winther, as it is
hermitian upon interchanging the forward and reverse directions.
We include, however,
a simple phase factor to keep it real-valued. The new deformation
parameter is called 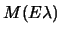 and has units of
and has units of
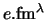 .
In terms of the Alder and Winther reduced matrix element it is
.
In terms of the Alder and Winther reduced matrix element it is
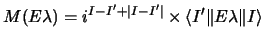 |
|
|
(85) |
and is directly related to the observable electro-magnetic transition
rate without any model-dependent parameters entering (except a sign):
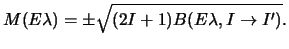 |
|
|
(86) |
A model dependent radius parameter Rc
only enters in the relation to the
deformation lengths of the rotational model:
 |
|
|
(87) |
for transitions from a state of spin I to one of spin I'
in a rotational band of projection K in a nucleus of charge Z.
Within K=0 bands,
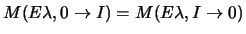 have the same sign as
have the same sign as
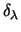 .
.
The only disadvantage of using reduced matrix elements as input parameters
in this way is
that the transitions in a rotational band do not all have the same
matrix elements
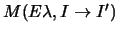 ,
even when the deformation length is constant.
,
even when the deformation length is constant.
The radial form factors for Coulomb inelastic processes may be simply
derived from the multipole expansion of
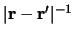 , giving
, giving
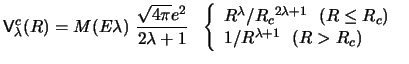 |
|
|
(88) |
remembering that a factor
 is already included in the matrix element
of equation (87) which appears in this form factor.
This form factor is to be multiplied by the angular momentum coupling
coefficients of the next section, and also by the charge of the
opposing nucleus.
is already included in the matrix element
of equation (87) which appears in this form factor.
This form factor is to be multiplied by the angular momentum coupling
coefficients of the next section, and also by the charge of the
opposing nucleus.
The basic rotational coupling coefficient, with
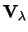 given by equation (70), is
given by equation (70), is
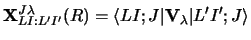 |
|
|
(89) |
The Coulomb form factors
 have
coupling coefficients
have
coupling coefficients
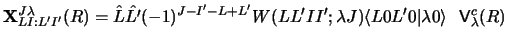 |
|
|
(90) |
whereas the nuclear form factors
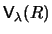 defined for
a rotational band with projection K have coupling coefficients
defined for
a rotational band with projection K have coupling coefficients
For projectile inelastic excitation, this coupling coefficient may be used
directly as
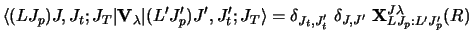 |
|
|
(92) |
whereas for target excitations,
| |
|
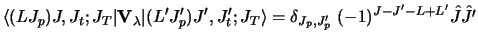 |
|
| |
|
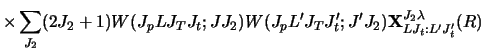 |
(93) |
When a nucleus consists of a single particle outside a core,
the state of the particle can be disturbed by the interaction with1
another nucleus, as the force of that nucleus can act differentially
on the particle and the core.
If
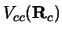 and
and
 are the interactions of the second nucleus with the
core and particle respectively,
then the excitation coupling from state
are the interactions of the second nucleus with the
core and particle respectively,
then the excitation coupling from state
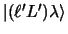 to state
to state
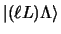 is given by the single-folding expression
is given by the single-folding expression
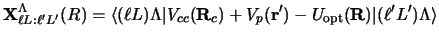 |
|
|
(94) |
where
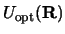 is the optical potential already defined for
these channels.
This optical potential is subtracted to avoid double counting of either
the Coulomb or the nuclear potentials,
rather than disabling the potentials which have already been defined.
This means that the `monopole' potential
is the optical potential already defined for
these channels.
This optical potential is subtracted to avoid double counting of either
the Coulomb or the nuclear potentials,
rather than disabling the potentials which have already been defined.
This means that the `monopole' potential
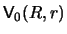 (to be constructed) will have no long-range Coulomb component,
and will not disturb the matching of the wave functions to the
asymptotic Coulomb functions.
It also means that if a nuclear well has already been defined,
the new monopole form factor will be simply the difference between this well
and that desired well calculated from the folding procedure.
(to be constructed) will have no long-range Coulomb component,
and will not disturb the matching of the wave functions to the
asymptotic Coulomb functions.
It also means that if a nuclear well has already been defined,
the new monopole form factor will be simply the difference between this well
and that desired well calculated from the folding procedure.
If the potentials
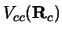 and
and
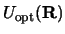 contain only scalar components, then
the R- and r- dependent Legendre multipole potentials
can be formed as
contain only scalar components, then
the R- and r- dependent Legendre multipole potentials
can be formed as
![$\displaystyle {\sf V}_K (R,r) =\frac{1}{2}\int_{-1}^{+1}
\left [ V_{cc} ({\bf R}_c) + V_p ({\bf r}') - U_{\rm opt} ({\bf R}) \right ]
. P_K (u) du$](img332.gif) |
|
|
(95) |
where
The coupling form factor between states 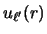 and
and 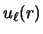 is then
is then
If the projectile has the particle - core composition, then the
coupling interaction is
 |
|
|
(97) |
where the initial (primed) and final (unprimed) states are
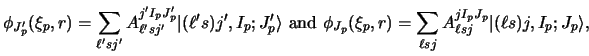 |
|
|
(98) |
respectively, and Ip is the (fixed) spin of the core.
Then
If the target has the particle - core composition, then the
coupling interaction is
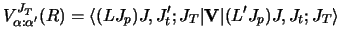 |
|
|
(100) |
where the initial (primed) and final (unprimed) states are
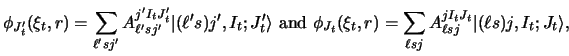 |
|
|
(101) |
respectively, and It is the (fixed) spin of the core in the target.
Then
4.4.1 Finite Range Transfers
To calculate the coupling term that arises when a particle is transferred,
for example from a target bound state to being bound in the projectile,
we need to evaluate source terms of the form
 |
|
|
(103) |
where the initial (primed) state has a composite target
with internal coordinates
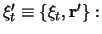
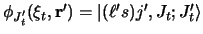 and the final (unprimed) state has a composite projectile
with internal coordinates
and the final (unprimed) state has a composite projectile
with internal coordinates
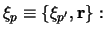
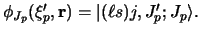
The 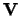 is the interaction potential, of which the prior form is
is the interaction potential, of which the prior form is
 |
|
|
(104) |
and the post form is
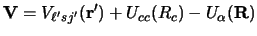 |
|
|
(105) |
where
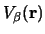 is the potential which binds
is the potential which binds
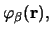
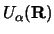 are the optical potentials, and
are the optical potentials, and
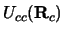 is the `core-core' potential, here between the p'
and the t nuclei.
The
is the `core-core' potential, here between the p'
and the t nuclei.
The 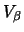 will be real, but the
will be real, but the 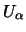 and
Ucc will typically have both real and imaginary components.
and
Ucc will typically have both real and imaginary components.
This source function 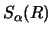 evaluates a non-local
integral operator, as it operates on the function
evaluates a non-local
integral operator, as it operates on the function
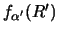 to produce a function of R.
This section therefore derives the non-local kernel
to produce a function of R.
This section therefore derives the non-local kernel
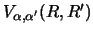 so that the source term, which initially involves a five
dimensional integral over
so that the source term, which initially involves a five
dimensional integral over 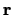 and
and 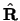 ,
may be calculated by means
of a one-dimensional integral over R':
,
may be calculated by means
of a one-dimensional integral over R':
 |
|
|
(106) |
Note that when the initial and final single-particle states are real, then
the kernel function is symmetric
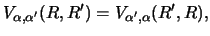 |
|
|
(107) |
whereas if the states are unbound and complex-valued, then the kernel
function is hermitian provided the interaction potential
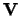 is real. If the particle states and the interaction potential
are complex, then both the forward and reverse kernels must be
each calculated independently.
is real. If the particle states and the interaction potential
are complex, then both the forward and reverse kernels must be
each calculated independently.
When the potential V contains only scalar potentials, the
kernel calculation can be reduced to the problem of finding
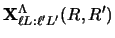 such that, given
such that, given
| |
|
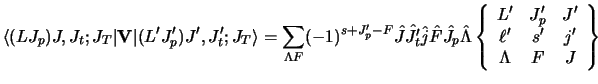 |
|
| |
|
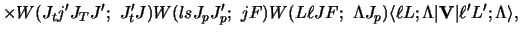 |
(108) |
the integral operator
 Note that the F summation may be performed in an inner loop that does
not evaluate the kernel function.
Note that the F summation may be performed in an inner loop that does
not evaluate the kernel function.
Now the 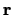 and
and 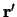 are linear combinations of the channel vectors
are linear combinations of the channel vectors
 and
and 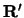 :
:
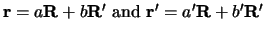 where,
when
where,
when
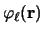 is the projectile bound state,
is the projectile bound state,
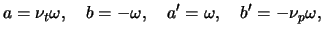 |
|
|
(109) |
with
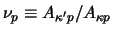 ,
,
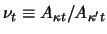 ,
and
,
and
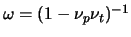 .
When
.
When
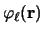 is the target bound state
is the target bound state
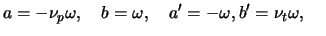 |
|
|
(110) |
with
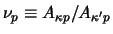 ,
,
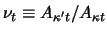 ,
and
,
and
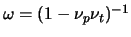 .
The `core-core' vector is always
.
The `core-core' vector is always
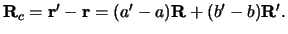
Thus the spherical harmonics
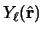 and
and
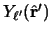 can be given in terms of the spherical harmonics
can be given in terms of the spherical harmonics
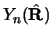 and
and
 by means of the Moshinsky [71]
solid-harmonic expansion (see also refs. [21]
and [46]
by means of the Moshinsky [71]
solid-harmonic expansion (see also refs. [21]
and [46]
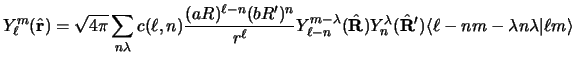 |
|
|
(111) |
where
with
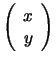 the binomial coefficient (Appendix A).
the binomial coefficient (Appendix A).
We now perform the Legendre expansion
 |
|
|
(112) |
where the Legendre polynomials PT (u)
are functions of u, the cosine of the angle between
 and
and 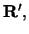 by using
r = (a2 R2 +b2 R'2 + 2abRR' u)1/2
(with r' analogously) in the numerical quadrature of the integral
by using
r = (a2 R2 +b2 R'2 + 2abRR' u)1/2
(with r' analogously) in the numerical quadrature of the integral
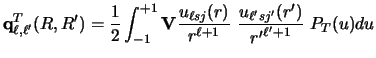 |
|
|
(113) |
The quadrature methods used here, and the accuracy attained, are
discussed in section 5.3.
Using the Legendre expansion, the radial kernel function
These formulae can also be used with
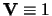 to calculate the kernel
functions
to calculate the kernel
functions
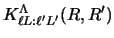 for the wave function overlap operator
for the wave function overlap operator
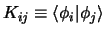 needed in evaluating the non-orthogonality terms of section 2.3.
needed in evaluating the non-orthogonality terms of section 2.3.
One disadvantage of this method of calculating the two-dimensional
radial kernels
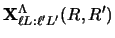 is that in the process of transforming the solid harmonics of
is that in the process of transforming the solid harmonics of
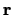 and
and 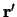 into those of
into those of
 and
and 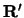 , there appears summations containing
high powers of the coefficients a, b, a' and b'
These products will become larger than unity by several orders of
magnitude, will the summed result is typically of the order of
unity. This means that
the summations involve large cancellations,
and as the degree of cancellation gets worse for large
, there appears summations containing
high powers of the coefficients a, b, a' and b'
These products will become larger than unity by several orders of
magnitude, will the summed result is typically of the order of
unity. This means that
the summations involve large cancellations,
and as the degree of cancellation gets worse for large
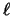 and
and 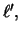 the cancellation places a limit
on the maximum value
the cancellation places a limit
on the maximum value 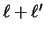 of the
transferred angular momentum.
of the
transferred angular momentum.
One way of circumventing this loss of accuracy is that proposed by
Tamura and Udagawa [47], whereby solid harmonics are avoided in favour of a suitable
choice of axes to render it practical to calculate m-dependent
form factors directly. If the 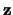 axis is not (as
usual) parallel to the incident momentum, but set parallel to
axis is not (as
usual) parallel to the incident momentum, but set parallel to
 , and the
, and the 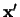 axis set in the plane determined
by
axis set in the plane determined
by  and
and 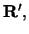 then the
then the 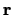 and
and 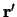 vectors are also in this plane.
The radial kernels may then be calculated as a sum of m-dependent
integrals over
vectors are also in this plane.
The radial kernels may then be calculated as a sum of m-dependent
integrals over
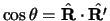 ,
as before the cosine of the angle between
,
as before the cosine of the angle between  and
and 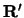 .
Although there are hence a larger number of radial integrals to be
performed, there are no large cancellations between the separate terms,
and there is no limit on the size of the transferred angular momentum.
.
Although there are hence a larger number of radial integrals to be
performed, there are no large cancellations between the separate terms,
and there is no limit on the size of the transferred angular momentum.
A third method [22]
of calculating the transfer form factors is that involving
expanding the initial and final channel wave functions in terms of
spherical Bessel functions:
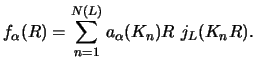 |
|
|
(115) |
Using then the Fourier transform of the bound state wave functions
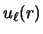 and
and
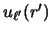 ,
a transfer T-matrix element may be written as a sum of a set of
one-dimensional integrals over a momentum variable.
Efficient codes [23]
have been written for CCBA calculations of transfers induced by light
ions (up to masses
,
a transfer T-matrix element may be written as a sum of a set of
one-dimensional integrals over a momentum variable.
Efficient codes [23]
have been written for CCBA calculations of transfers induced by light
ions (up to masses 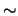 10 to 15 amu).
10 to 15 amu).
This plane-wave expansion method has however several disadvantages when
it comes to solving problems with coupled reaction channels. If
transfers are to be calculated at each iteration of the coupled
equations, then the expansion (115) has to be recalculated at each step.
Another difficulty is that the method is not suited to heavy-ion induced
transfers, as the large degree of absorption inside the nuclei in these
cases requires a large number of momentum basis states Kn
to be represented accurately. The plane-wave expansion becomes
uneconomical, and sometimes the determination of the
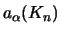 coefficients becomes numerically ill-conditioned
coefficients becomes numerically ill-conditioned
We will see in section 5.3.1, however, that
if the cancellation which occurs in the first method is monitored,
and steps taken to keep it to a minimum, a workable code
[34]
results which can produce accurate results for L-transfers up to around 6.
When the projectile wave functions
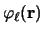 are all s-states (
are all s-states (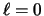 and
the interaction potential is of zero-range
and
the interaction potential is of zero-range
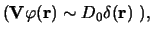 then the form factor
then the form factor
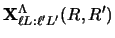 of equation (114) can be simplified to
of equation (114) can be simplified to
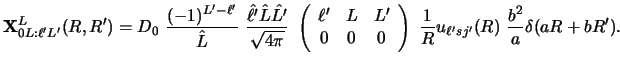 |
|
|
(116) |
This can be made local by defining a new step size
 in the stripping channel
in the stripping channel 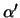 .
.
If the interaction potential is of small range, though not zero,
and the projectile still contains only s-states,
then a first-order correction may be made to the above form factor.
This correction will depend on the rate of oscillation of the source wave
function
fJT (L' J'p),J' ,J't (R' )
within a `finite-range effective radius' 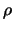 .
The rate of oscillation is estimated from the local energy
in the entrance and exit channels,
and the result [24]
is to replace
.
The rate of oscillation is estimated from the local energy
in the entrance and exit channels,
and the result [24]
is to replace
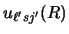 in the previous section by
in the previous section by
![$\displaystyle u_{\ell' sj'} (R) \rightarrow
u_{\ell' sj'} (R)
\left [ 1 + \rho^...
...'} ( R) + V_{\ell' sj'} (R)
-U _\alpha (R) + \epsilon _\alpha \right ) \right ]$](img421.gif) |
|
|
(117) |
where the U(R) are the optical potentials, with
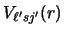 the single-particle binding potential in the target.
The
the single-particle binding potential in the target.
The
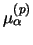 is the reduced mass of the particle in the projectile,
and
is the reduced mass of the particle in the projectile,
and
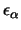 its binding energy.
its binding energy.
At sub-Coulomb incident energies [25], the details of the nuclear potentials
in equation (117) become invisible, and as the longer-ranged Coulomb
potentials cancel by charge conservation, the form factor can be simplified to
![$\displaystyle D_0 u_{\ell' sj'} (R) \rightarrow
u_{\ell' sj'} (R) D_0
\left [ 1 + \rho^2 {2 \mu _\alpha^{(p)}\over \hbar^2} \epsilon _\alpha \right ]$](img425.gif) |
= |
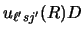 |
(118) |
where
![$\displaystyle D = D_0 \left [ 1 + \left ( \rho k _\alpha^{(p)} \right ) ^2 \right ]$](img427.gif) |
|
|
(119) |
is the effective zero-range coupling constant for sub-Coulomb transfers.
The parameters D0 and D can be derived
from the details of the projectile bound state
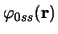 .
The zero-range constant D0 may be defined as
.
The zero-range constant D0 may be defined as
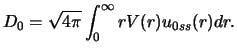 |
|
|
(120) |
The parameter D, on the other hand, reflects the asymptotic
strength of the wave function u0ss (r) as
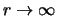 ,
as it is the magnitude of this tail which is important in sub-Coulomb reactions:
,
as it is the magnitude of this tail which is important in sub-Coulomb reactions:
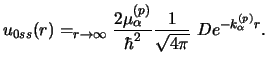 |
|
|
(121) |
It may be also found, using Schrödinger's equation, from the
integral
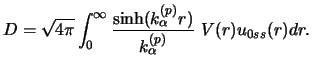 |
|
|
(122) |
From this equation we can see that as the range of the potential becomes smaller,
D approaches D0. The `finite-range effective radius'
 of equation (119) is thus some measure of the mean radius
of the potential V(r).
of equation (119) is thus some measure of the mean radius
of the potential V(r).


Next: 5 Numerical Solutions
Up: Coupled Reaction Channels Calculations
Previous: 3 Wave Functions for
Prof Ian Thompson
2004-05-09
![]() , then there can be
higher-order tensor interactions which couple together the spin and the
orbital motion. If a nucleus has spin
, then there can be
higher-order tensor interactions which couple together the spin and the
orbital motion. If a nucleus has spin
![]() , then there can be
a spin-orbit component
, then there can be
a spin-orbit component
![]() in the
Hamiltonian
in the
Hamiltonian ![]() . and if its spin is one or greater
(
. and if its spin is one or greater
(![]() ), there can be tensor forces of various kinds.
The most commonly used tensor force is a Tr potential
of the form
), there can be tensor forces of various kinds.
The most commonly used tensor force is a Tr potential
of the form
![]() .
Similar tensor forces are also generated if the projectile and target
spins coupled together can reach
.
Similar tensor forces are also generated if the projectile and target
spins coupled together can reach
![]() :
such is the case with the tensor force between the proton and the neutron
within the deuteron.
:
such is the case with the tensor force between the proton and the neutron
within the deuteron.
![]() + 2H, or
7Li =
+ 2H, or
7Li =![]() + 3H. In all these cases, there arise
inelastic potentials which can re-orient the ground state of the
composite nucleus, or can excite the valence particle into higher-energy
eigenstates.
+ 3H. In all these cases, there arise
inelastic potentials which can re-orient the ground state of the
composite nucleus, or can excite the valence particle into higher-energy
eigenstates.
![]() in equation (30). They also require that the coupled equations be solved
by iteration, as will be discussed in section 5.
If the effects of recoil are neglected, the `no-recoil' (NR)
approximation is obtained, but in general[72]
this is inaccurate in ways which are difficult to predict. For that reason
the NR approximation is not included in the present code.
For many light-ion reactions, however, another `zero-range'
approximation is available, and this does remove many of the finite-range
requirements. Alternatively, a first-order correction for the finite-range
effects may be estimated, to give the `local energy approximation'.
These two special cases are discussed at the end of the section.
in equation (30). They also require that the coupled equations be solved
by iteration, as will be discussed in section 5.
If the effects of recoil are neglected, the `no-recoil' (NR)
approximation is obtained, but in general[72]
this is inaccurate in ways which are difficult to predict. For that reason
the NR approximation is not included in the present code.
For many light-ion reactions, however, another `zero-range'
approximation is available, and this does remove many of the finite-range
requirements. Alternatively, a first-order correction for the finite-range
effects may be estimated, to give the `local energy approximation'.
These two special cases are discussed at the end of the section.
![]() which multiply these matrix elements are not
specified, since these are usually determined by a fitting procedure
in an optical-model search code, and a wide variety of
parameterised forms have been used.
which multiply these matrix elements are not
specified, since these are usually determined by a fitting procedure
in an optical-model search code, and a wide variety of
parameterised forms have been used.
![]() representation
for the order of coupling the spins, as in equation (24).
representation
for the order of coupling the spins, as in equation (24).
![]()
![$\displaystyle = \delta_{L L'} \delta_{ J_1 J'_1 }
\frac{1}{2}[ J_1 ( J_1 +1) - L(L+1) - J_p( J_p+ 1) ]$](img261.gif)
![]() , we first transform
, we first transform
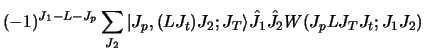
![\begin{eqnarray*}\nonumber
&&\left\langle (L J_p ) J_1 , J_t ; J_T \vert {\bf L\...
...ta_{L L' }\frac{1}{2}[ J_2 ( J_2 +1) - L(L+1) - J_t ( J_t + 1) ]
\end{eqnarray*}](img270.gif)

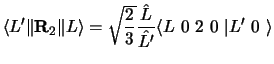
![]() tensor force
tensor force
![]() the coupling interactions are
the coupling interactions are
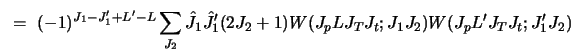
![]() tensor force
tensor force
![]() the coupling interactions are
the coupling interactions are
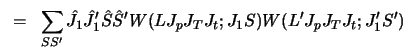
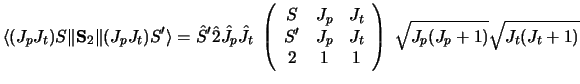
![]() .
The effect of these deformations can be expressed as a change in the radius
at which we evaluate the optical potentials, the change depending on the
relative orientations of the radius vector to the intrinsic orientation
of the nucleus. Deformation lengths are used to specify the these
changes, rather than fractional deformations
.
The effect of these deformations can be expressed as a change in the radius
at which we evaluate the optical potentials, the change depending on the
relative orientations of the radius vector to the intrinsic orientation
of the nucleus. Deformation lengths are used to specify the these
changes, rather than fractional deformations ![]() ,
to remove a dependence on the `average potential radius'
RU. This is desirable because often the real and imaginary
parts of the potential have different radii, and it is not clear which is
to be used. It also removes a dependence on exactly how the `average
radius' of a potential is to be defined.
,
to remove a dependence on the `average potential radius'
RU. This is desirable because often the real and imaginary
parts of the potential have different radii, and it is not clear which is
to be used. It also removes a dependence on exactly how the `average
radius' of a potential is to be defined.
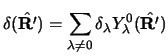
![]() are small, the above multipole functions
are simply the first derivatives of the U(R) function:
are small, the above multipole functions
are simply the first derivatives of the U(R) function:
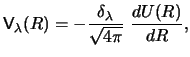
![]() , but unfortunately an average potential radius is
again introduced. The dependence on models for average radii can be
reduced by defining the Coulomb deformations in terms of a reduced matrix
element such as that of Brink and Satchler [19], or that of Alder and Winther
[20].
For the present purposes we adopt that of Alder and Winther, as it is
hermitian upon interchanging the forward and reverse directions.
We include, however,
a simple phase factor to keep it real-valued. The new deformation
parameter is called
, but unfortunately an average potential radius is
again introduced. The dependence on models for average radii can be
reduced by defining the Coulomb deformations in terms of a reduced matrix
element such as that of Brink and Satchler [19], or that of Alder and Winther
[20].
For the present purposes we adopt that of Alder and Winther, as it is
hermitian upon interchanging the forward and reverse directions.
We include, however,
a simple phase factor to keep it real-valued. The new deformation
parameter is called ![]() and has units of
and has units of
![]() .
In terms of the Alder and Winther reduced matrix element it is
.
In terms of the Alder and Winther reduced matrix element it is
![]() ,
even when the deformation length is constant.
,
even when the deformation length is constant.
![]() , giving
, giving
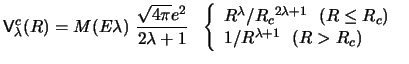
![]() given by equation (70), is
given by equation (70), is
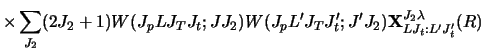
![]() and
and
![]() are the interactions of the second nucleus with the
core and particle respectively,
then the excitation coupling from state
are the interactions of the second nucleus with the
core and particle respectively,
then the excitation coupling from state
![]() to state
to state
![]() is given by the single-folding expression
is given by the single-folding expression
![]() and
and
![]() contain only scalar components, then
the R- and r- dependent Legendre multipole potentials
can be formed as
contain only scalar components, then
the R- and r- dependent Legendre multipole potentials
can be formed as
![$\displaystyle {\sf V}_K (R,r) =\frac{1}{2}\int_{-1}^{+1}
\left [ V_{cc} ({\bf R}_c) + V_p ({\bf r}') - U_{\rm opt} ({\bf R}) \right ]
. P_K (u) du$](img332.gif)
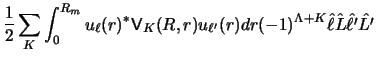
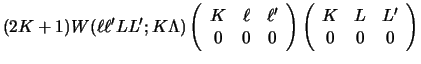
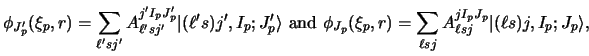
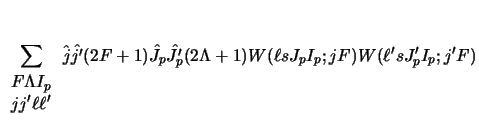
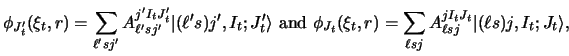

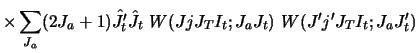
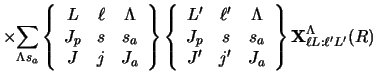

![]() is the interaction potential, of which the prior form is
is the interaction potential, of which the prior form is
![]() evaluates a non-local
integral operator, as it operates on the function
evaluates a non-local
integral operator, as it operates on the function
![]() to produce a function of R.
This section therefore derives the non-local kernel
to produce a function of R.
This section therefore derives the non-local kernel
![]() so that the source term, which initially involves a five
dimensional integral over
so that the source term, which initially involves a five
dimensional integral over ![]() and
and ![]() ,
may be calculated by means
of a one-dimensional integral over R':
,
may be calculated by means
of a one-dimensional integral over R':
![]() such that, given
such that, given
![]() and
and ![]() are linear combinations of the channel vectors
are linear combinations of the channel vectors
![]() and
and ![]() :
:
![]() where,
when
where,
when
![]() is the projectile bound state,
is the projectile bound state,
![]() and
and
![]() can be given in terms of the spherical harmonics
can be given in terms of the spherical harmonics
![]() and
and
![]() by means of the Moshinsky [71]
solid-harmonic expansion (see also refs. [21]
and [46]
by means of the Moshinsky [71]
solid-harmonic expansion (see also refs. [21]
and [46]
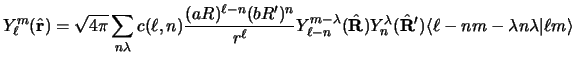
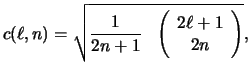
 the binomial coefficient (Appendix A).
the binomial coefficient (Appendix A).

![]() is that in the process of transforming the solid harmonics of
is that in the process of transforming the solid harmonics of
![]() and
and ![]() into those of
into those of
![]() and
and ![]() , there appears summations containing
high powers of the coefficients a, b, a' and b'
These products will become larger than unity by several orders of
magnitude, will the summed result is typically of the order of
unity. This means that
the summations involve large cancellations,
and as the degree of cancellation gets worse for large
, there appears summations containing
high powers of the coefficients a, b, a' and b'
These products will become larger than unity by several orders of
magnitude, will the summed result is typically of the order of
unity. This means that
the summations involve large cancellations,
and as the degree of cancellation gets worse for large
![]() and
and ![]() the cancellation places a limit
on the maximum value
the cancellation places a limit
on the maximum value ![]() of the
transferred angular momentum.
of the
transferred angular momentum.
![]() axis is not (as
usual) parallel to the incident momentum, but set parallel to
axis is not (as
usual) parallel to the incident momentum, but set parallel to
![]() , and the
, and the ![]() axis set in the plane determined
by
axis set in the plane determined
by ![]() and
and ![]() then the
then the ![]() and
and ![]() vectors are also in this plane.
The radial kernels may then be calculated as a sum of m-dependent
integrals over
vectors are also in this plane.
The radial kernels may then be calculated as a sum of m-dependent
integrals over
![]() ,
as before the cosine of the angle between
,
as before the cosine of the angle between ![]() and
and ![]() .
Although there are hence a larger number of radial integrals to be
performed, there are no large cancellations between the separate terms,
and there is no limit on the size of the transferred angular momentum.
.
Although there are hence a larger number of radial integrals to be
performed, there are no large cancellations between the separate terms,
and there is no limit on the size of the transferred angular momentum.
![]() coefficients becomes numerically ill-conditioned
coefficients becomes numerically ill-conditioned
![]() are all s-states (
are all s-states (![]() and
the interaction potential is of zero-range
and
the interaction potential is of zero-range
![]() then the form factor
then the form factor
![]() of equation (114) can be simplified to
of equation (114) can be simplified to
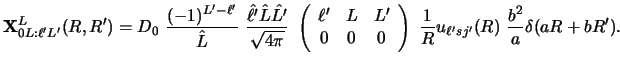
![]() .
The rate of oscillation is estimated from the local energy
in the entrance and exit channels,
and the result [24]
is to replace
.
The rate of oscillation is estimated from the local energy
in the entrance and exit channels,
and the result [24]
is to replace
![]() in the previous section by
in the previous section by
![$\displaystyle D_0 u_{\ell' sj'} (R) \rightarrow
u_{\ell' sj'} (R) D_0
\left [ 1 + \rho^2 {2 \mu _\alpha^{(p)}\over \hbar^2} \epsilon _\alpha \right ]$](img425.gif)
![]() .
The zero-range constant D0 may be defined as
.
The zero-range constant D0 may be defined as