

Next: 3 Wave Functions for
Up: Coupled Reaction Channels Calculations
Previous: 1 Introduction
Subsections
The coupled reaction channels (CRC) model of direct reactions in nuclear
physics proceeds by constructing a model of the system wave function, and
solving Schrödinger's equation as accurately as possible within
that model space. The model used here projects the complete wave function
 onto a product
onto a product
 of projectile and target states with a wave function
of projectile and target states with a wave function
 describing their relative motion:
describing their relative motion:
 |
|
|
(1) |
The basis states  and
and  can be bound states
of their respective nuclei,
or they may be discrete representations of continuum levels.
In the former case we have a `bound state approximation',
and in the second case we have a `coupled discrete continuum channels'
[39,40] (CDCC) approximation.
The states
can be bound states
of their respective nuclei,
or they may be discrete representations of continuum levels.
In the former case we have a `bound state approximation',
and in the second case we have a `coupled discrete continuum channels'
[39,40] (CDCC) approximation.
The states  can be in different mass partitions, or they
can be different excited states of the projectile and/or the target in any
one of the partitions.
What is essential to the CRC framework is that there be a finite set (N
say) of square-integrable basis states, as this leads to a finite set of
equations coupling the channel wave functions
can be in different mass partitions, or they
can be different excited states of the projectile and/or the target in any
one of the partitions.
What is essential to the CRC framework is that there be a finite set (N
say) of square-integrable basis states, as this leads to a finite set of
equations coupling the channel wave functions
 as unknowns.
as unknowns.
For a complete Hamitonian
 and total energy E,
Schrödinger's equation
and total energy E,
Schrödinger's equation
![$ [ \overline{{\cal H} } - E ]\overline{\Psi } = 0$](img9.gif) becomes
becomes
![$ [ {\cal H} - E ]\Psi = 0$](img10.gif) in the model space with [6]
in the model space with [6]
 |
|
|
(2) |
where
 and
and 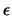 is a positive infinitesimal quantity whose presence ensures that
the excluded channels have a time-retarded propagator, and hence only
remove flux from the model space.
The second term as a whole describes the effects of the excluded channels on
the model subspace
is a positive infinitesimal quantity whose presence ensures that
the excluded channels have a time-retarded propagator, and hence only
remove flux from the model space.
The second term as a whole describes the effects of the excluded channels on
the model subspace
 . These effects could be, for example,
from compound nucleus formation, which we have excluded from explicit
consideration within direct reaction theory.
In the absence of detailled knowledge of these effects, we construct our
model Hamiltonian
. These effects could be, for example,
from compound nucleus formation, which we have excluded from explicit
consideration within direct reaction theory.
In the absence of detailled knowledge of these effects, we construct our
model Hamiltonian 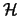 using effective potentials which we believe
approximate (in some average manner) the processes described by equation
(2). The effective potentials will often be optical potentials with
real and imaginary components fitted to some simpler kinds of reactions,
and the effects of compound nucleus formation on these potentials is to
contribute to their imaginary component.
using effective potentials which we believe
approximate (in some average manner) the processes described by equation
(2). The effective potentials will often be optical potentials with
real and imaginary components fitted to some simpler kinds of reactions,
and the effects of compound nucleus formation on these potentials is to
contribute to their imaginary component.
The model Hamiltonian 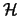 for the CRC system can now be projected
onto the individual basis states
for the CRC system can now be projected
onto the individual basis states  . If Ei
is the asymptotic kinetic energy in the i'th channel, then the
channel-projected Hamiltonian Hi satisfies
. If Ei
is the asymptotic kinetic energy in the i'th channel, then the
channel-projected Hamiltonian Hi satisfies
 |
|
|
(3) |
and will be composed of a kinetic energy term and a diagonal optical
potential. The `interaction potential' Vi is then
defined to be everything in 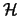 not included in Hi, so
not included in Hi, so
 |
|
|
(4) |
This construction gives Vi which have vanishing diagonal matrix
elements
 .
.
If we take the model Schrödinger's equation
![$ [ {\cal H} - E ]\Psi = 0, $](img19.gif) and project separately onto the
different basis states
and project separately onto the
different basis states  we derive the set of equations
we derive the set of equations
![$\displaystyle \left [ E_i - H_i \right ]\psi_i ( {\bf R}_i ) =
\sum _ {j \neq i...
...\langle\phi_i \vert {\cal H}-E \vert\phi_j \right\rangle
\psi_j ( {\bf R}_j ) .$](img21.gif) |
|
|
(5) |
which couple together the unknown wave functions
 The matrix element
The matrix element
 has two different forms, depending on whether we expand
has two different forms, depending on whether we expand
Thus
where
 |
|
|
(7) |
The overlap function
 in
equation (6) arises from the well-known non-orthogonality between the
basis states
in
equation (6) arises from the well-known non-orthogonality between the
basis states  and
and  if these are in
different mass partitions. We will see below that this term disappears in
first-order DWBA, and can be made to disappear in second-order DWBA, if
the first and second steps use the prior and post interactions
respectively.
if these are in
different mass partitions. We will see below that this term disappears in
first-order DWBA, and can be made to disappear in second-order DWBA, if
the first and second steps use the prior and post interactions
respectively.
If the coupling interactions Vi in equation (6) are
weak, or if the back coupling effects of these interactions are already
included in the optical potentials of the prior channel, then it becomes
reasonable to use a distorted wave Born approximation (DWBA). This
approximation always feeds flux `forwards' in the sequence
 neglecting the back couplings. In
the elastic channel the wave function is governed by the optical potential
defined there, and the wave function in the i'th channel is
governed by the equation
neglecting the back couplings. In
the elastic channel the wave function is governed by the optical potential
defined there, and the wave function in the i'th channel is
governed by the equation
![$\displaystyle \left [ E_i - H_i \right ]\psi_i ( {\bf R}_i ) =
\sum _ {j=1} ^ {...
...ft\langle\phi_i \vert {\cal H}-E \vert\phi_j \right\rangle
\psi_j ( {\bf R}_j )$](img35.gif) |
|
|
(8) |
Initial channel:
Second channel:
![$\displaystyle \left [ E_2 - H_2 \right ]\psi_2 ( {\bf R}_2 ) =
\left\langle\phi_2 \vert {\cal H}-E \vert\phi_1 \right\rangle
\psi_1 ( {\bf R}_1 )$](img37.gif) |
|
|
(9) |
If the prior interaction is used, the right hand side becomes
Final channel: (c=N+1)
![$\displaystyle \left [ E_c - H_c \right ]\psi_c ( {\bf R}_c ) =
\sum _ {j=1} ^{j...
...ft\langle\phi_c \vert {\cal H}-E \vert\phi_j \right\rangle
\psi_j ( {\bf R}_j )$](img41.gif) |
|
|
(12) |
If the post interaction
had been used for all the couplings to this last channel, then
![$\displaystyle \left [ E_c - H_c \right ]\psi_c ( {\bf R}_c ) =
\sum_ {j=1} ^ {j...
..._j
+ [H_c - E_c ]~ \sum_{j=1} ^ {j=c-1}
\langle\phi_c \vert\phi_j\rangle \psi_j$](img42.gif) |
|
|
(13) |
so
![$\displaystyle \left [ E_c - H_c \right ] \chi_c ( {\bf R}_c ) =
\sum_{j=1} ^ {j=c-1}
V_{cj}^{\rm post} \psi_j$](img43.gif) |
|
|
(14) |
where
Note that, as all the  are square-integrable
and hence decay faster than r -1 at large radii,
the
are square-integrable
and hence decay faster than r -1 at large radii,
the  and
and  are the same asymptotically.
They differ only by an `off-shell transformation',
and hence yield the same (on-shell) scattering amplitudes.
The equation for
are the same asymptotically.
They differ only by an `off-shell transformation',
and hence yield the same (on-shell) scattering amplitudes.
The equation for  has no non-orthogonality terms once
the post interaction is used in the final channel:
this is what is meant by saying that the final channel is
`effectively on-shell'.
has no non-orthogonality terms once
the post interaction is used in the final channel:
this is what is meant by saying that the final channel is
`effectively on-shell'.
These results imply that in N-step DWBA, some non-orthogonality terms
can be made to
disappear if `prior' interactions are used for the first step, and/or if
`post' interactions are used for the final step. This means that the
non-orthogonality term never appears in the first-order DWBA, irrespective
of the choice of prior or post forms. In second-order DWBA, the
prior-post combination must be chosen [7]
to avoid the non-orthogonality
terms. It should be also clear that non-orthogonality terms will have to
be evaluated if the DWBA is continued beyond second order.
2.3 Full CRC solution by iteration
There are a number of different ways of solving the CRC equations with the
non-orthogonality terms present: for discussions of different approaches see refs.
[8], [41] and the survey of ref.[ch. 3][33].
There are schemes available which can
iterate all channels with an arbitrary choice of post or
prior interactions for all the couplings.
Define
The following iterative scheme
[42]
(n=1,2,..) on convergence then solves the CRC equations (5):
For n =0, start with
For
 (for N-step DWBA) solve
(for N-step DWBA) solve
![$\displaystyle [ H_i - E_i ] \chi_i^{(n)} + S_i^{(n-1)} = 0$](img58.gif) |
|
|
(19) |
with
![$\displaystyle S_i^{(n-1)} = \sum _ j
[ \theta_{ij} V_{ij}^{\rm post} + (1 - \theta_{ij} ) V_{ij}^{\rm prior} ] ~
\psi_j^{(n-1)} - \delta S_i^{(n-1)}$](img59.gif) |
|
|
(20) |
then calculate for subsequent iterations
This scheme avoids numerical differentations except in an higher-order
correction to  that arises in some circumstances.
that arises in some circumstances.
When the non-orthogonality terms are included properly, it becomes merely
a matter of convenience whether post or prior couplings are used,
for one, two, and multistep calculations.
The equivalence of the two coupling forms can be confirmed in practice
(see, for example, refs.[42], and [9]),
and used as one check on the accuracy of the numerical methods employed.


Next: 3 Wave Functions for
Up: Coupled Reaction Channels Calculations
Previous: 1 Introduction
Prof Ian Thompson
2004-05-09
![]() onto a product
onto a product
![]() of projectile and target states with a wave function
of projectile and target states with a wave function
![]() describing their relative motion:
describing their relative motion:
![]() and total energy E,
Schrödinger's equation
and total energy E,
Schrödinger's equation
![]() becomes
becomes
![]() in the model space with [6]
in the model space with [6]
![]() for the CRC system can now be projected
onto the individual basis states
for the CRC system can now be projected
onto the individual basis states ![]() . If Ei
is the asymptotic kinetic energy in the i'th channel, then the
channel-projected Hamiltonian Hi satisfies
. If Ei
is the asymptotic kinetic energy in the i'th channel, then the
channel-projected Hamiltonian Hi satisfies
![]() and project separately onto the
different basis states
and project separately onto the
different basis states ![]() we derive the set of equations
we derive the set of equations
![]() neglecting the back couplings. In
the elastic channel the wave function is governed by the optical potential
defined there, and the wave function in the i'th channel is
governed by the equation
neglecting the back couplings. In
the elastic channel the wave function is governed by the optical potential
defined there, and the wave function in the i'th channel is
governed by the equation
![$\displaystyle \left [ E_i - H_i \right ]\psi_i ( {\bf R}_i ) =
\sum _ {j=1} ^ {...
...ft\langle\phi_i \vert {\cal H}-E \vert\phi_j \right\rangle
\psi_j ( {\bf R}_j )$](img35.gif)
![$\displaystyle \left [ E_c - H_c \right ]\psi_c ( {\bf R}_c ) =
\sum _ {j=1} ^{j...
...ft\langle\phi_c \vert {\cal H}-E \vert\phi_j \right\rangle
\psi_j ( {\bf R}_j )$](img41.gif)
![$\displaystyle \left [ E_c - H_c \right ]\psi_c ( {\bf R}_c ) =
\sum_ {j=1} ^ {j...
..._j
+ [H_c - E_c ]~ \sum_{j=1} ^ {j=c-1}
\langle\phi_c \vert\phi_j\rangle \psi_j$](img42.gif)
![$\displaystyle \left [ E_c - H_c \right ] \chi_c ( {\bf R}_c ) =
\sum_{j=1} ^ {j=c-1}
V_{cj}^{\rm post} \psi_j$](img43.gif)

![$\displaystyle S_i^{(n-1)} = \sum _ j
[ \theta_{ij} V_{ij}^{\rm post} + (1 - \theta_{ij} ) V_{ij}^{\rm prior} ] ~
\psi_j^{(n-1)} - \delta S_i^{(n-1)}$](img59.gif)

![$\displaystyle \sum _ j (1-\theta_{ij})
\langle\phi_i \vert\phi_j\rangle
[ S_j^{(n-1)} + [H_j - E_j ] \delta\psi_j^{(n)} ]$](img63.gif)