3 Runtime errors

In a complicated modeling computer program like FRESCO, accurate results cannot be obtained if there are obvious numerical errors either in the input, or produced during the calculation. Problems may occur at energies very much below the Coulomb barrier, or at relativistic energies, since FRESCO should not be used in these cases. The program is written to stop when large numerical inaccuracies occur, but no results can be trusted until they are examined to see that they are not sensitive to further increases to the maximum radius rmatch, maximum partial waves jtmax, maximum non-local range rnl, and further decreases in the radial step size hcm and lower radial cutoff parameter cutl. We give some guidance on these parameters below.

When the program reads the input file, typing errors in variables or their values will cause the program to stop after printing out the complete namelist so you can see which variables have been successfully read in. Alternatively, if the words NAMELIST and CDCC in the second line of the input are written in lower case (`namelist' or `cdcc'), the compiler's own error handling will be used instead. You can also look at the input echo in fort.3, to see up to which line the input has been read successfully.

During the running of FRESCO, a number of induced or cancellation errors can be detected. These are:

Step size too large:

If k is the asymptotic wave number for a channel, then its product with the step size should be sufficiently small for the Numerov integration method to avoid large errors: k*hcm < 0.2.

Bound-state search failure:

Bound states are found in subroutine eigcc by a Newton-Raphson method with at most 40 iterations. Such states can be found at a specific energy by varying some part of the potential: this part cannot be zero.

Insufficient non-local width:

If the non-local coupling form factors are too large when 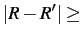$\vert R-R'\vert \ge$ rnl, then rnl should be increased as recommended.

L-transfer accuracy loss:

In the transfer Legendre expansion, if 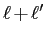$\ell+\ell'$ is too large, there can be cancellation errors between different multipoles T. This can be remedied by increasing the input parameter mtmin to use the slower m-dependent method of [1].

Matching deficiency:

The program will print an error message if the nuclear potentials are not smaller than 0.02 MeV at the outer matching radius, and stop if they are larger than 0.1 MeV. Increase rmatch, or correct some potential that does not decay sufficiently fast.

Iteration failure in solving coupled equations:

If in some partial wave set, more than iter iterations still do not appear to converge, then all cross sections will be affected. Either use Padé acceleration, increase iter or make it negative so that the `best' intermediate value is used, or increase ips slightly. The detailed progress of the iterations can be seen by setting smats $\ge 5$.

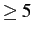Accuracy loss in solving coupled equations:

If any of the channels are propagating in a classically forbidden region, there will be loss of linear independence of the separate solutions 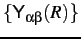$\{{\sf Y}_{\alpha\beta}(R)\}$, as all solutions will tend to become exponentially increasing. This is monitored in the subroutine erwin during the summations, and will lead to a halt if the cancellation errors are expected to be more than 3%. In this case, increase the lower cutoff parameters cutl or cutr, decrease the matching radius rmatch if possible, or else use the R-matrix expansion method to solve the equations. An extreme error occurs if the simultaneous equations from the matching conditions are singular.

Internal parameter error:

Sometimes, the precalculation of array sizes is inadequate. For advanced users these can be improved by selective specification of the maxcoup(1:3) and expand(1:11) input arrays.

At the end of a FRESCO calculation, a final `accuracy analysis' is presented. This rechecks that the step size hcm is small enough, and that rnl is large enough. Then, using the Coulomb trajectories, it calculates the minimum scattering angles expected to be accurate because of the finite values of rmatch and jtmax.