This section discusses the methods used to solve the coupled reaction
channels equations (30), when in general there are both local
couplings
![]() and non-local kernels
and non-local kernels
![]() .
Now a group of m equations can be solved `exactly' (subject only
to radial discretisation errors) by finding [53]
a set of m linearly independent groups of solutions
gi,k (R), and taking a linear combination of these which satisfies
the required boundary conditions.
This method is only practicable, however, if there are not too many
equations (the numerical effort can rise as m3), and if there
are only local couplings. For in that case the independent solutions can
be found in a single outward `sweep' of m2 radial
functions. Non-local couplings mean, unfortunately, that the source terms
at a given radius depend on the wave functions at other radii both larger
and smaller, so that this `exact' method becomes impractical.
.
Now a group of m equations can be solved `exactly' (subject only
to radial discretisation errors) by finding [53]
a set of m linearly independent groups of solutions
gi,k (R), and taking a linear combination of these which satisfies
the required boundary conditions.
This method is only practicable, however, if there are not too many
equations (the numerical effort can rise as m3), and if there
are only local couplings. For in that case the independent solutions can
be found in a single outward `sweep' of m2 radial
functions. Non-local couplings mean, unfortunately, that the source terms
at a given radius depend on the wave functions at other radii both larger
and smaller, so that this `exact' method becomes impractical.
In many cases of interest in nuclear physics, however, the non-local couplings are not too strong, and can be treated as successive perturbations. They can then be applied iteratively until further applications have progressively smaller efffects, and the solutions have converged (to some preset criterion of accuracy). Some failures of convergence can remedied by the use of Padé approximants.
When both local and non-local couplings are present, and the local couplings are too strong to allow an iterative scheme to converge, a combination of the exact and iterative schemes is possible. In this approach, several channels can be `blocked' together, and treated as one unit during the iterations, while solving the couplings within the block by the exact method.
There are several other features of typical nuclear reaction calculations which simplify the numerical methods:
If the non-local interactions
![]() in the CRC equations (30) are present, then it will always be necessary
to solve the coupled channels by iteration. With the local couplings
in the CRC equations (30) are present, then it will always be necessary
to solve the coupled channels by iteration. With the local couplings
![]() however, we have a choice
whether to iterate, or to include them in the exact solutions of
the close-coupling method. A simple option is to allow a specifiable
number b of channels to be coupled
exactly, with the remainder only being fed after one or more iterations.
This would be useful, for example, if the channels for the low-lying
states of a highly-deformed target were included in this block of b
channels, and if the remaining channels (e.g. for transfers) were not fed
by more than 2 or 3 steps beyond this initial block.
Restricting these iterations to one is equivalent to solving a CCBA model.
however, we have a choice
whether to iterate, or to include them in the exact solutions of
the close-coupling method. A simple option is to allow a specifiable
number b of channels to be coupled
exactly, with the remainder only being fed after one or more iterations.
This would be useful, for example, if the channels for the low-lying
states of a highly-deformed target were included in this block of b
channels, and if the remaining channels (e.g. for transfers) were not fed
by more than 2 or 3 steps beyond this initial block.
Restricting these iterations to one is equivalent to solving a CCBA model.
Whether the coupled equations are of the simpler form of equation (30),
or of the more complex form of section 2.3, a particular n'th
iteration will require solving set of m equations of the form
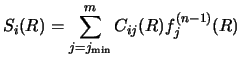 |
(125) |
These coupled differential equations can be solved, following the method
of ref. [53] by forming the linearly independent solution
sets gi,k (R), where the k'th solution consists of
a set of all channels (![]() ) which is made independent of
the other sets by having a distinctive starting value
) which is made independent of
the other sets by having a distinctive starting value
The independent solutions gi,k (R) are required for m+1
values of k. The solution vectors for ![]() are solved
starting with equation (126) but with no source term in
the equation (123): these will contribute to the complementary
solution of the homogeneous equation.
We also need a particular solution gi,0 (R) of the
inhomogeneous equation, solved with the source terms but with
no non-zero values in equation (126). These partial
solutions may be conveniently laid out as in figure 5.1.
If, however, it is known that the wave functions of certain channels are
not required (if, for example, they are only fed in the last iteration),
then it is not necessary to store their components in the array, for their
S-matrix elements can still be calculated.
are solved
starting with equation (126) but with no source term in
the equation (123): these will contribute to the complementary
solution of the homogeneous equation.
We also need a particular solution gi,0 (R) of the
inhomogeneous equation, solved with the source terms but with
no non-zero values in equation (126). These partial
solutions may be conveniently laid out as in figure 5.1.
If, however, it is known that the wave functions of certain channels are
not required (if, for example, they are only fed in the last iteration),
then it is not necessary to store their components in the array, for their
S-matrix elements can still be calculated.
The solutions fi (R) are the linear combination of the
gi,k (R)
 |
Note that the independent solutions gi,k (R) for ![]() need only be calculated the first time this coupled channels
set is used. If they are stored as in figure 5.1,
subsequent iterations need only recalculate the first row (IT=1)
as the source terms vary. Furthermore, if there are multiple incoming
channels for fixed total spin JT and parity
need only be calculated the first time this coupled channels
set is used. If they are stored as in figure 5.1,
subsequent iterations need only recalculate the first row (IT=1)
as the source terms vary. Furthermore, if there are multiple incoming
channels for fixed total spin JT and parity ![]() , then
solutions after the first can also use the gi,k (R) already
stored. The first iteration for these subsequent incoming channels will in
fact not require any radial integrations whatsoever, merely finding a new
set of { ak } from the new matching conditions,
and recalculating the sum (127) if the
wave functions are required.
, then
solutions after the first can also use the gi,k (R) already
stored. The first iteration for these subsequent incoming channels will in
fact not require any radial integrations whatsoever, merely finding a new
set of { ak } from the new matching conditions,
and recalculating the sum (127) if the
wave functions are required.
Tolsma and Veltkamp [54]
point out one difficulty with this method, which is that if the couplings
Ci,j are strong for ![]() , then the linear
independence of the gi,j (R) will be reduced as R
increases through a classically forbidden region. This is because the
components with negative local kinetic energy will generally consist of an
exponentially growing part and an exponentially decreasing part. The
former is responsible for the tendency to destroy the initially generated
linear independence of the solution vectors. The longer the integration
continues through a classically forbidden region, the stronger this
tendency will be; for instance, it will occur in scattering problems of
nuclear physics with energies near or below the Coulomb barrier. It will
also occur if inelastic form factors are used which are not approximately
derivatives of the diagonal potential, but which extend more than usual
into the interior of the nucleus that is classically forbidden because
of the centrifugal potentials.
, then the linear
independence of the gi,j (R) will be reduced as R
increases through a classically forbidden region. This is because the
components with negative local kinetic energy will generally consist of an
exponentially growing part and an exponentially decreasing part. The
former is responsible for the tendency to destroy the initially generated
linear independence of the solution vectors. The longer the integration
continues through a classically forbidden region, the stronger this
tendency will be; for instance, it will occur in scattering problems of
nuclear physics with energies near or below the Coulomb barrier. It will
also occur if inelastic form factors are used which are not approximately
derivatives of the diagonal potential, but which extend more than usual
into the interior of the nucleus that is classically forbidden because
of the centrifugal potentials.
Tolsma et al. [54] propose a stabilization procedure to monitor and if necessary re-orthogonalise the solution vectors. If this were not done, there would be large cancellations in the sum of equation (127), resulting if severe in complete loss of accuracy of the S-matrix elements and the solution wave functions.
A simpler approach is to increase the starting radius ![]() at which the radial integrations begin. It is advisable in any case for
reasons of stability at small radii to have a minimum radius proportional to
some angular momentum
at which the radial integrations begin. It is advisable in any case for
reasons of stability at small radii to have a minimum radius proportional to
some angular momentum ![]() typical of the coupled channels set:
typical of the coupled channels set:
The iterative method of solving the CRC equations (5, 30)
will converge if the couplings are sufficiently small.
The procedure will however diverge if the the couplings are too large, or if
the system is too near a resonance.
On divergence, the successive wave functions ![]() will become larger and larger as n increases, and not converge to
any fixed limit. Unitarity will of course be violated as the S-matrix
elements will become much larger than unity.
will become larger and larger as n increases, and not converge to
any fixed limit. Unitarity will of course be violated as the S-matrix
elements will become much larger than unity.
There are several ways of dealing with this problem:
The method (2) is not used because of the size of the matrix that results. Initially, the matrix would be sparse, with selected elements away from the diagonal being non-zero because of the coupling potentials. The kinetic energy operators occupy a band of width three along the diagonal. Although a Gaussian elimination procedure would allow potentials of arbitrary coupling strength to be included, it will fill in large regions of the matrix as the solution proceeds, and this makes the storage requirements prohibitive.
The separable expansion method (3), while useful for light-ion reactions, is unsatisfactory for heavy-ion transfers. This is because if the masses of the initial and final nuclei become large relative to the mass of the transferred particle, the form factor for the transfers becomes more nearly local. As we approach the no-recoil limit (which makes the form factors exactly local) a separable expansion of a nearly-local kernel will require a large number of terms. In the limit of a local form factor, the separable expansion will require the same number of terms as there are radial points.
The method (4) of expanding the wave functions in Gaussians
could have been used, provided the characteristic widths in R-space
of the basis states were chosen in accordance with the wave number
![]() in the relevant channel.
This requirement is less severe with light-ion reactions, where the
wave numbers are typically
in the relevant channel.
This requirement is less severe with light-ion reactions, where the
wave numbers are typically ![]() fm-1.
For heavy-ion reactions, however, the oscillation rates are much larger,
and a more sensible method is to expand in terms of Airy functions
that are depend explicitly on the local wave number over some radial region.
fm-1.
For heavy-ion reactions, however, the oscillation rates are much larger,
and a more sensible method is to expand in terms of Airy functions
that are depend explicitly on the local wave number over some radial region.
It is very useful to be able to iterate the coupled equations in a conventional manner, as then 1, 2 and 3 step DWBA results (etc.) can be recovered by stopping the iterations short of full convergence. This recovery of DWBA results is more difficult with sequential iteration (6), but both that method and the method of (7) would be definitely advantageous when, say, exciting a long rotational band by successive application of a quadrupole coupling. Using Padé acceleration has the advantages that it need only be employed if ordinary iterations are seen to diverge, and that it transforms the previously-divergent results with little new computational effort.
A given sequence
![]() of S-matrix elements
that result from iterating the CRC equations
can be regarded as the successive partial sums of the polynomial
of S-matrix elements
that result from iterating the CRC equations
can be regarded as the successive partial sums of the polynomial
| (129) |
![$\displaystyle P_{[n,m]} (\lambda) = {p_0 + p_1 \lambda + p_2 \lambda^2 + \cdots + p_n \lambda^n
\over
1 + q_1 \lambda + q_2 \lambda^2 + \cdots + q_m \lambda^m }$](img462.gif) |
(130) |
There are many different ways [48]
of evaluating the coefficients
{pm , qn}, but for the present problem we can use
Wynn's ![]() -algorithm [31], which is a method of evaluating
the upper right half of the Padé table at
-algorithm [31], which is a method of evaluating
the upper right half of the Padé table at ![]() =1 directly
in terms of the original sequence
=1 directly
in terms of the original sequence
![]() .
.
Initialising
![]() and
and
![]() ,
we form an array
using the relation
,
we form an array
using the relation
![]() Thus we can construct the table given the second column from the initial sequence
Sj.
The table then gives the transposed upper right half of the Padé table,
including the diagonal:
Thus we can construct the table given the second column from the initial sequence
Sj.
The table then gives the transposed upper right half of the Padé table,
including the diagonal:
| (131) |
When accelerating a vector S-matrix elements
![]() , with a component for each coupled channel,
then it is important to accelerate the vector as a whole.
Wynn [32]
pointed out that this can be done using the Samuelson inverse
, with a component for each coupled channel,
then it is important to accelerate the vector as a whole.
Wynn [32]
pointed out that this can be done using the Samuelson inverse
| (132) |
As discussed in section 4.4.1,
the summations over T in equation (114) involve large cancellations,
and as the degree of cancellation gets worse for large
![]() and
and ![]() , this places a limit
on the maximum value
, this places a limit
on the maximum value ![]() of the
transferred angular momentum.
of the
transferred angular momentum.
Typically, however, the transfer form factors are only needed to be accurate to
around 0.1 to 1%,
so if computer arithmetic is used which is accurate to 14 or
16 decimal digits, then cancellations up to 12 or 13 orders of magnitude
should in principle not result in catastrophic errors in the transfer
rates. With careful programming, this accuracy can be achieved.
What is necessary is to be careful that all quantities in the equations
(114, 113) above which depend on the Legendre order T are calculated
to the full computer precision. It is not necessary, for example,
for the channel wave functions ![]() , the bound
state wave functions
, the bound
state wave functions
![]() or the
quadrature of the integral (113) to be accurate to full precision
(which in any case would be impossible). It is only necessary
that all these quantities have exactly the same computer
precision when the coefficients over T (the
or the
quadrature of the integral (113) to be accurate to full precision
(which in any case would be impossible). It is only necessary
that all these quantities have exactly the same computer
precision when the coefficients over T (the
![]() are evaluated,
and when the sums over T (in equation 114) are performed.
This will require principally that the `radial framework' that gives
are evaluated,
and when the sums over T (in equation 114) are performed.
This will require principally that the `radial framework' that gives
![]() and
and ![]() in terms of
in terms of ![]() and
and ![]() be accurate to full machine precision, as also the Racah algebra
coefficients in equation (114). In fact, the channel wave functions
be accurate to full machine precision, as also the Racah algebra
coefficients in equation (114). In fact, the channel wave functions
![]() and the bound state wave functions
and the bound state wave functions
![]() may be calculated with reduced precisions
using shorter computer words and faster arithmetic should
these be available. It is also not necessary for the coefficients and sums
over T be consistent to full accuracy for different R and
R' values, as the large cancellations only occur between
different T values for each separate R and R' combination.
may be calculated with reduced precisions
using shorter computer words and faster arithmetic should
these be available. It is also not necessary for the coefficients and sums
over T be consistent to full accuracy for different R and
R' values, as the large cancellations only occur between
different T values for each separate R and R' combination.
Since the accuracy of the quadrature in the equation (113) is not critical
to the overall accuracy of the transfers, calculations may be speeded up if we
economise on the range of the u variable and on the
number of intermediate steps required.
Even in light ion reactions it is not necessary to integrate u to -1
(![]() to 180
to 180![]() ) as was done in the code LOLA
[72]
for example. An efficient procedure to adopt is that used in the DWBA
code DAISY[55], where, for each successive R value, the code monitors the rate
of decay of the integrand as
) as was done in the code LOLA
[72]
for example. An efficient procedure to adopt is that used in the DWBA
code DAISY[55], where, for each successive R value, the code monitors the rate
of decay of the integrand as ![]() increases. For a given accuracy
criterion, an estimate can then be made of an adequate upper limit
for the
increases. For a given accuracy
criterion, an estimate can then be made of an adequate upper limit
for the ![]() integration at the next R value. Typically, the upper
limits of
integration at the next R value. Typically, the upper
limits of ![]() decrease monotonically as R increases from 0 to the
upper limit Rm.
Because the integrand is largest for
decrease monotonically as R increases from 0 to the
upper limit Rm.
Because the integrand is largest for ![]() =0, the accuracy of the angular
integration for small
=0, the accuracy of the angular
integration for small ![]() is improved by a change of variable from u
to x as in ref.[55]:
is improved by a change of variable from u
to x as in ref.[55]:
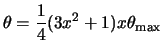 |
(133) |
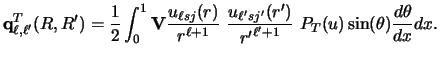 |
(134) |
The methods used to calculate, store and use the non-local form factors
![]() (equation 113) and
(equation 113) and
![]() (equation 108)
have to be efficient in a wide variety of reactions, from light-ion
reactions such as
3He(3H,4He)2H or 16O(20Ne,24Mg)12C
to heavy-ion reactions, such as nickel on tin one-nucleon transfers.
In the former cases, the radial form factors
(equation 108)
have to be efficient in a wide variety of reactions, from light-ion
reactions such as
3He(3H,4He)2H or 16O(20Ne,24Mg)12C
to heavy-ion reactions, such as nickel on tin one-nucleon transfers.
In the former cases, the radial form factors
![]() will be non-zero over large regions of the R-R' space, so
(following ref [56]) interpolation procedures should prove effective.
will be non-zero over large regions of the R-R' space, so
(following ref [56]) interpolation procedures should prove effective.
However, when small masses are transferred between two larger nuclei
the form factor is nearly local, and only large around
![]() If the whole (R,R') array had to be calculated and stored in
these cases,
modelling heavy-ion transfers would become inefficient,
even with interpolation methods.
The form factor now varies rapidly as a function of
If the whole (R,R') array had to be calculated and stored in
these cases,
modelling heavy-ion transfers would become inefficient,
even with interpolation methods.
The form factor now varies rapidly as a function of
![]() (especially for heavy ion reactions,
as the Jacobian b3 in equation (114) becomes large),
and varies only slowly with R (if
(especially for heavy ion reactions,
as the Jacobian b3 in equation (114) becomes large),
and varies only slowly with R (if ![]() is constant),
as this variation follows the radial dependence of the bound state
wave functions.
The best procedure is thus [56]
to first change to the coordinate pair
is constant),
as this variation follows the radial dependence of the bound state
wave functions.
The best procedure is thus [56]
to first change to the coordinate pair
![]() and R, and then to use different interpolatory
intervals
and R, and then to use different interpolatory
intervals ![]() and hR in the two directions
respectively. Then, when nuclear masses become large compared with the mass
of the transferred particle,
and hR in the two directions
respectively. Then, when nuclear masses become large compared with the mass
of the transferred particle, ![]() can become smaller,
perhaps even smaller than h, the basic radial step size.
can become smaller,
perhaps even smaller than h, the basic radial step size.
The method adopted in FRESCO is to let the user specify
![]() and hR as multiples or
submultiples of h. The value of hR is very often always 3 to 5
times larger than h, as this reflects the typical rate at which bound
state wave functions vary.
If the bound state wave functions have many internal nodes, then the
interpolation interval hR cannot be so large
(this is often the case with
and hR as multiples or
submultiples of h. The value of hR is very often always 3 to 5
times larger than h, as this reflects the typical rate at which bound
state wave functions vary.
If the bound state wave functions have many internal nodes, then the
interpolation interval hR cannot be so large
(this is often the case with ![]() -particle bound states).
-particle bound states).
The ![]() on the other hand, will be larger than h for light-ion reactions
(as described in [47]), but will be comparable with or smaller than
h for few-nucleon transfers between heavy ions. The user also
specifies the maximum and minimum values of the range of
on the other hand, will be larger than h for light-ion reactions
(as described in [47]), but will be comparable with or smaller than
h for few-nucleon transfers between heavy ions. The user also
specifies the maximum and minimum values of the range of ![]() which again will be large (
which again will be large ( ![]() nuclear radii) for light ions,
and small (
nuclear radii) for light ions,
and small ( ![]() 1 or 2 fm.) for heavy ion reactions. The accuracy of these
choices is checked retrospectively by collecting statistics on the
distributions of the functions
1 or 2 fm.) for heavy ion reactions. The accuracy of these
choices is checked retrospectively by collecting statistics on the
distributions of the functions
![]() averaging
over R. and all partial waves T,
averaging
over R. and all partial waves T, ![]() , and
, and ![]()
When ![]() or hR are multiples h,
then (say) cubic splines in two dimensions can be used to expand the form
factors for the integrals of equation (106).
If, however,
or hR are multiples h,
then (say) cubic splines in two dimensions can be used to expand the form
factors for the integrals of equation (106).
If, however, ![]() is a submultiple h,
as is the case in many heavy-ion reactions,
then a more efficient procedure is possible.
is a submultiple h,
as is the case in many heavy-ion reactions,
then a more efficient procedure is possible.
Suppose, say, we wish to evaluate the numerical integral
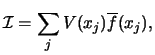 |
(135) |
| (136) |
| = | 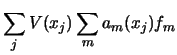 |
(137) | |
| = | (138) |
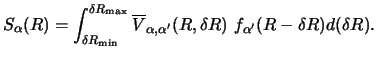 |
(140) |
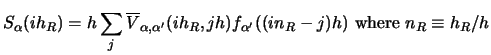 |
(141) |
Simultaneous Two-Nucleon Transfers:
A similar `preemptive' summation is possible when calculating the
form factors for the simultaneous transfer of two nucleons between states
of the form of equation (50) in the projectile and in the target.
As mentioned in section 3.4,
two-nucleon transfer can be viewed as the transfer of a
`structured particle' with internal coordinates
![]() and
and
![]() , the distance between the two nucleons. A transfer is only possible
if the initial and final states have identical values for these `internal
coordinates'. The angular momentum quantum numbers can be matched
exactly, but source terms can either be constructed for each
, the distance between the two nucleons. A transfer is only possible
if the initial and final states have identical values for these `internal
coordinates'. The angular momentum quantum numbers can be matched
exactly, but source terms can either be constructed for each ![]() value and summed in equation (106),
or the separate
value and summed in equation (106),
or the separate ![]() products can be summed as early as equation (113).
Because the separate
products can be summed as early as equation (113).
Because the separate ![]() values are only used in a summation,
it is most economical to use Gaussian quadrature,
as for a given accuracy this reduces by a half
the number of rhoi values at which the wave functions of equation
(50) need to be calculated and stored.
If the rhoi are chosen to be the Gaussian quadrature points over
some chosen range, and if wi are the corresponding weights,
the equation (113) becomes
values are only used in a summation,
it is most economical to use Gaussian quadrature,
as for a given accuracy this reduces by a half
the number of rhoi values at which the wave functions of equation
(50) need to be calculated and stored.
If the rhoi are chosen to be the Gaussian quadrature points over
some chosen range, and if wi are the corresponding weights,
the equation (113) becomes
![$\displaystyle {\bf q}^T_ {L , L'} (R,R') =
\frac{1}{2}\int_ {-1}^{+1}
r^{-L-1} ...
...[ \sum _ i w_i {\bf V} u_{12} (r, \rho_i) ~
u'_{12} (r' , \rho_i) ]
P_T (u) du.$](img504.gif) |
(142) |
I would like to thank Dr. Nagarajan, John Lilley, Ray Mackintosh, Victoria Andres and a referee for valuable questions and comments at various stages in this project. Manchester University, Daresbury Laboratory, the Niels Bohr Institute, and Bristol University are thanked for their hospitality when these ideas were being developed, and the Department of Engineering Mathematics at Bristol is thanked for their assistance in the preparation of this paper.